ตัวอย่างเรื่องที่ ๑ เกมกระดาษ กรรไกร และค้อน

เด็กๆ แทบทุกคนรู้จักการเล่นชนิดหนึ่ง คือ เมื่อแบมือจะหมายถึง กระดาษ ชูเฉพาะนิ้วชี้ และ นิ้วกลางจะหมายถึง กรรไกร และ ถ้ากำมือจะหมายถึง ค้อน เมื่อให้สัญญาณแล้วทั้ง 2 ฝ่ายก็จะแสดงท่าพร้อมๆ กันโดยมีเงื่อนไขว่า
 

กระดาษ ชนะ ค้อน แพ้ กรรไกร

กรรไกร ชนะ กระดาษ แพ้ ค้อน

ค้อน ชนะ กรรไกร แพ้ กระดาษ

ถ้าออกท่าเดียวกันถือว่าเสมอ

 

ในที่นี้จะแสดงการหาความน่าจะเป็น หรือ โอกาสที่ผู้เล่นควรออกท่าใด จึงจะดีที่สุด

ขั้นที่ 1 

เพื่อความสะดวกในการคำนวณ ให้ 1 แทนการชนะ -1 แทนแพ้ และ 0 แทนการเสมอกัน สมมุติดำ และ แดงเล่นเกมนี้ จะได้ตารางแสดงผลการออกท่าต่างๆ เมื่อคิดทางฝ่ายดำ คือ

 

		แดง
		กรรไกร	กระดาษ	ค้อน
ดำ	กรรไกร	0	1	-1
	กระดาษ	-1	0	1
	ค้อน	1	-1	0

 

ทั้งนี้ เพราะ ถ้าดำออกกรรไกร แดงออกกรรไกรก็จะเสมอ ผลจึงเป็น 0 สำหรับดำ และ แดง

ถ้าดำออกกรรไกร แดงออกกระดาษ กรรไกรจะชนะกระดาษ ผลจึงเป็น 1 สำหรับ ดำ

ถ้าดำออกกรรไกร แดงออกค้อน กรรไกรจะแพ้ค้อน ผลจึงเป็น 1 สำหรับดำ ทำนองเดียวกัน สำหรับการออกท่าอื่นๆ ของดำ

ขั้นที่ 2

 

หาค่าความแตกต่างระหว่างแถว โดยที่ต่างฝ่ายต่างไม่ทราบว่า อีกฝ่ายจะออกท่าใด จึงควรพิจารณาจากความแตกต่างของผล ที่อาจเกิดขึ้น ของอีกฝ่ายหนึ่ง เช่น แดงควรคำนึงถึงผลต่างในการออกท่าของดำตามแถว ดังนี้
 

		แดง
		กรรไกร	กระดาษ	ค้อน
ดำ	กรรไกร-กระดาษ	1	1	-2
	กระดาษ-ค้อน	-2	1	1

ขั้นที่ 3 

หาสัดส่วนที่แดงควรออกท่าแต่ละท่า เมื่อจะหาน้ำหนักที่ควรออกท่าใด ให้ปิดเท่านั้น แล้วหาค่าของการคูณทแยงตัวเลขที่เหลือ เช่น สัดส่วนที่แดงควรออกท่ากรรไกร คำนวณได้จากตัวเลขในช่องกระดาษ และ ค้อน

"ค่าของการคูณทแยง" คำนวณได้จากการคูณตัวเลขตามลูกศรลงแล้วลบด้วย ผลคูณของตัวเลขในแนวลูกศรขึ้น จะได้ (1 x 1) - 1 x ( - 2 ) = 1 + 2 = 3

ทำนองเดียวกัน หาน้ำหนัก หรือ สัดส่วนของการที่แดงจะออกกระดาษได้ จากการปิดช่องกระดาษ แล้วหาค่าของการคูณทแยงตัวเลขในช่องที่เหลือ จากช่องกระดาษ คือ ตัวเลขที่อยู่ในช่องกรรไกร และ ค้อน (...)

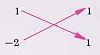
จะได้ (1 x 1) -(-2) x (-2) = 1 - 4 -3

สำหรับน้ำหนักของการที่แดงจะออกค้อน คือ ค่าที่ได้จากการคูณทแยงตัวเลข ที่ไม่อยู่ในช่องค้อน ซึ่งได้แก่

จะได้ (1 x 1) -(-2 x 1) = 1 + 2 = 3

ผลที่ได้จากการคูณทแยงทั้งสาม โดยไม่คิดเครื่องหมาย คือ สัดส่วนที่แดงควรออกท่ากรรไกร กระดาษ แ ละค้อน ซึ่งได้แก่ 3 : 3 : 3 หรือ 1: 1 : 1 แสดงว่า แดงควรออกท่าใดก็ได้ด้วยโอกาสเท่าๆ กัน คือ 1/3 จะทำให้ค่าเฉลี่ยของผลที่แดงจะเสียให้ดำ ไม่ว่าดำจะออกท่าใดก็ตาม เหมือนกันหมดคือ 0 โดยคำนวณได้ดังนี้
 

ถ้าดำออกกรรไกร และ แดงออกกรรไกร หรือ กระดาษ หรือ ค้อน ด้วยโอกาสเท่าๆ กัน ค่าเฉลี่ยของผลที่แดงจะเสียให้ดำ คือ

 

(1/3 x 0) + (1/3 x 1) + 1/3 x (-1) = 0

ถ้าดำออกกระดาษ ค่าเฉลี่ยดังกล่าว คือ

1/3 x (-1) + (1/3 x 0) + (1/3 x 1) = 0

ทำนองเดียวกันถ้าดำออกค้อน ค่าเฉลี่ยที่แดงจะเสียให้ดำ คือ

(1/3 x 1) + 1/3 x (-1) + (1/3 x 0) = 0

 

เมื่อพิจารณาทางฝ่ายของดำ ไม่ว่าดำจะออกเท่าใด เขาจะต้องเปรียบเทียบผลที่ควรได้จากท่าทีแดงออก นั่นคือ ผลต่างในลำดับเดียวกันของค่าในช่องกรรไกรกับกระดาษ และ ช่องกระดาษกับค้อน ดังนี้

 

 

		แดง
ดำ	กรรไกร	-1	2
	กระดาษ	-1	-1
	ค้อน	2	-1

เช่นเดียวกับที่คำนวณมาแล้ว ทางฝ่ายแดงจะได้สัดส่วนของดำที่จะออกท่ากรรไกร โดยการคำนวณจากผลคูณทแยงของค่าที่ไม่อยู่ในแถว กรรไกร คือ

จะได้ (-1) x (-1) -(-2) x (-1) = 1 + 2 = 3

สัดส่วนของดำที่จะออกท่ากระดาษ คำนวณได้จากผลคูณทแยงของตัว เลขที่ไม่อยู่ในแถวกระดาษ คือ

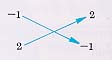
จะได้ (-1) x (-1) - (2 x 2) = 1 - 4 = -3

สัดส่วนของดำที่จะออกท่าค้อน คำนวณได้จากผลคูณทแยงของตัวเลขที่ ไม่อยู่ในแถวค้อน

จะได้ (-1) x (-1) - (-1) x 2 = 1 + 2 = 3

ฉะนั้นสัดส่วนที่ดำควรออกท่ากรรไกร : กระดาษ : ค้อน คือ 3 : 3 : 3 หรือ 1 : 1 : 1 ไม่ว่าแดงจะออกท่าใดก็ตาม จะทำให้ค่าเฉลี่ยที่ดำจะได้จากเกมนี้ เท่ากันหมด คือ 0

ทั้งนี้เพราะถ้าแดงออกท่ากรรไกร ไม่ว่าดำจะออกกรรไกร หรือ กระดาษ หรือค้อน ด้วยโอกาสเท่าๆ กันคือ 1/3 โดยเฉลี่ยแล้ว ผลที่ดำจะได้รับ คือ
 

(1/3 x 0) + 1/3 x (-1) + (1/3 x 1) = 0

 

ถ้าแดงออกท่ากระดาษไม่ว่าดำจะออกท่าใด โดยเฉลี่ยแล้วผลที่ดำจะ ได้รับ คือ

 

(1/3 x 1) + (1/3x 0) + 1/3 x (-1) = 0

 

ทำนองเดียวกันสำหรับการออกท่าค้อนของแดง โดยเฉลี่ยแล้วผลที่ดำ จะได้รับ คือ

 

1/3 x (-1) + (1/3 x 1) + (1/3 x 0) = 0

จากค่าเฉลี่ยของผลที่แต่ละฝ่ายจะได้รับ เมื่อเล่นด้วยความน่าจะเป็นเท่าๆ กันคือ 1 ซึ่งหมายถึง การออกท่าใดก็ได้นั้น ทำให้เกมนี้เป็นเกมที่ยุติธรรม เพราะ ไม่มีฝ่ายใดได้เปรียบ หรือ เสียเปรียบ การที่ฝ่ายใดชนะหรือแพ้ ขึ้นอยู่กับความบังเอิญอย่างเดียว

อาจเป็นที่สงสัยว่า การที่ฝ่ายใดจะออกท่ากรรไกร กระดาษ หรือ ค้อนด้วย ความน่าจะเป็นเท่าๆ กัน คือ 1/3 นั้น จะทำอย่างไร ในทางปฏิบัติจะเทียบกับการ กระทำอย่างอื่นที่มีโอกาสเกิดผลเท่ากันคือ 1/3 เช่น ทำสลาก 3 ใบ เขียนใน ใบหนึ่งว่า กรรไกร อีกใบหนึ่งเขียนว่ากระดาษ และ ใบสุดท้ายเขียนว่าค้อน แล้ว ม้วนหรือพับกระดาษแต่ละใบนั้น เพื่อไม่ให้มองเห็นตัวหนังสือที่เขียนไว้ก่อน จะจับสลากนี้แต่ละครั้งต้องเขย่าหรือเคล้าให้คละกัน เพื่อให้โอกาสที่จะหยิบใบใดๆ ขึ้นมาได้มีค่า 1/3 เมื่อหยิบแล้วผลที่ได้เป็นอย่างไรก็ออกท่าตามที่ปรากฏนั้น ซึ่ง ก็จะมีความน่าจะเป็น 1/3 เหมือนกับที่หยิบสลาก หรือ จะใช้การโยนลูกเต๋า โดย พิจารณาผลที่จะมีโอกาสเกิดขึ้นได้ 1/3 เท่าๆ กัน เช่น ถ้าลูกเต๋าหงายหน้าหนึ่ง หรือ หน้าสอง จะออกท่ากรรไกร ถ้าลูกเต๋าหงายหน้าสาม หรือ หน้าสี่ จะออกท่า กระดาษ และ ถ้าลูกเต๋าหงายหน้าห้า หรือ หน้าหกจะออกท่าค้อน ก็จะทำให้โอกาส ที่จะออกท่าใดๆ มีค่า 1/3 เช่นเดียวกับการที่ลูกเต๋าจะหงายหน้าหนึ่ง หรือ หน้าสอง หรือ หน้าอื่นดังกล่าว แต่เด็กส่วนมากมักจะออกท่าใดก็ได้ โดยไม่ต้องจับสลาก หรือ ทอดลูกเต๋า 

โดยใช้ความรู้ในเรื่องความน่าจะเป็น จะทำให้สามารถหาสัดส่วน หรือ ความน่าจะเป็นที่แต่ละฝ่ายควรเล่นสำหรับเกมใดๆ ได้เสมอ ในกรณีที่ค่าเฉลี่ยของแต่ละฝ่ายที่จะได้รับ หรือ เสียไม่ใช่ 0 แสดงว่าเกมนั้นไม่ยุติธรรม เมื่อทราบว่าฝ่ายใดจะได้เปรียบ ก็มีทางที่จะคิดค่าเล่นล่วงหน้า เพื่อทำให้เกมยุติธรรมได้ 

สำหรับเกมอื่นๆ ที่มีจำนวนวิธีที่ต่างฝ่ายจะเล่นได้มากกว่าสามอย่าง ก็มีวิธีคิดหาแผนการเล่นที่ดีที่สุดแตกต่างไป ผู้ที่สนใจจะศึกษาได้จากหนังสือชื่อ The Compleat Strategyst ซึ่งมี เจ ดี วิลเลียมส์ (J.D. Williams) เป็นผู้ประพันธ์ และ ถ้าสนใจจะศึกษาทฤษฎีทางคณิตศาสตร์ที่ซับซ้อน และ ที่อธิบายวิธีคิดหาแผน การเล่นที่ดีที่สุดดังกล่าว ก็อาจศึกษาได้ จากหนังสือที่เกี่ยวกับทฤษฎีของเกม