บทนำ 

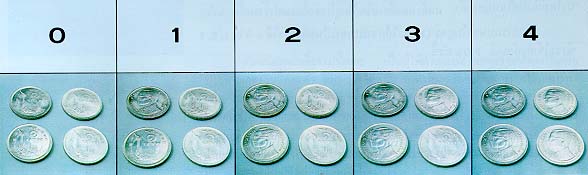
ตราบใดที่มีความไม่แน่นอน หรือ การคาดคะเนจะมีเรื่องของ "ความน่าจะเป็น" เกี่ยวข้องด้วยเสมอ ค่าของความน่าจะเป็นช่วยบอกให้ทราบล่วงหน้าได้ว่า เรื่องที่ไม่แน่นอนนั้นจะมีโอกาสเกิดขึ้นได้มากน้อยเพียงไหน เช่น ในการหยิบสลาก 1 ใบ จากสลาก 10 ใบ เราบอกไม่ได้แน่นอนว่า จะหยิบได้ใบไหน แต่โอกาสที่จะหยิบได้ใบใดย่อมมีเหมือนๆ กัน คือ 1 ใน 10 ใบ เรียกค่า 1/10 นี้ว่า "ค่าของความน่าจะเป็นใน การหยิบสลาก 1 ใบ"

ทำนองเดียวกัน ถ้าในกล่องหนึ่งมีของเหมือนๆ กันอยู่ 100 ชิ้น และ ทราบว่าปกติจะมีของเสียประมาณ 5 ชิ้น รวมปนอยู่โดยมองไม่เห็นด้วยตาเปล่าว่าชิ้นใดเสีย เมื่อหยิบของนั้นมา 1 ชิ้น โอกาสที่จะได้ของเสียจะมีอยู่ 5 ใน 100 เรียกค่า 5/100 นี้ว่า ค่าของความน่าจะเป็นในการหยิบได้ของที่เสีย 1 ชิ้น ถ้ามีของเสียหลายชิ้น โอกาสที่หยิบของ 1 ชิ้น และ พบว่าเสียย่อมมีมาก ถ้าเสียทั้ง 100 ชิ้นเมื่อหยิบขึ้นมา 1 ชิ้น การที่จะได้ของเสียย่อมเกิดขึ้นแน่ ค่า100/100 หรือ 1 คือ ค่าของความน่าจะเป็น ที่จะได้ของเสีย ซึ่งเป็นค่าความน่าจะเป็นของเหตุการณ์ ที่เกิดขึ้นแน่นอน และ ถ้าในของ 100 ชิ้นนั้น ไม่มีของเสียเลย โอกาสที่หยิบของมาชิ้นหนึ่งแล้ว จะพบว่าเป็นของเสีย ย่อมไม่เกิดขึ้นแน่ ค่า 0/100 หรือ 0 หรือค่าของความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้ ค่าของความน่าจะเป็นที่สำคัญอันดับแรกมี 3 ประเภท คือ 

ค่าของความน่าจะเป็นของเหตุการณ์ใดๆ อยู่ระหว่าง 0 กับ 1

ค่าของความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้นแน่มีค่าเป็น 1

ค่าของความน่าจะเป็นของเหตุการณ์ที่เป็นไปไม่ได้มีค่าเป็น 0

 

ก่อนที่จะคำนวณความน่าจะเป็น จะต้องพิจารณาเหตุการณ์ที่เกิดขึ้นว่า อยู่ในลักษณะใด ค่าของความน่าจะเป็นจะต้องเป็นทศนิยม หรือ เศษส่วน มีค่าระหว่าง 0 ถึง 1 จะเป็น 0 เมื่อลักษณะนั้นเกิดขึ้นไม่ได้เลย จะมีค่าเป็น 1 เมื่อลักษณะนั้นเกิดขึ้นอย่างแน่นอน

 

 

 

ความน่าจะเป็นของเหตุการณ์หนึ่ง = ทางที่เป็นไปได้ / ทางทั้งหมด

ดังตัวอย่างเช่น  ลักษณะของแต้มคู่ที่ปรากฏบนลูกเต๋าธรรมดา เนื่องจากแต้มคู่มี 3 ด้าน ทางที่เป็นไปได้จึงเป็น 3 ลูกเต๋ามีด้านทั้งหมด 6 ด้าน ทางทั้งหมดจึงเป็น 6

ความน่าจะเป็นที่จะให้ได้แต้มคู่ = 3/6 = 1/2

ในด้านการจัดการอาจจะต้องใช้ความน่าจะเป็นตามโอกาสที่เกิดขึ้น เช่น ต้องการตอบคำถามว่า "โอกาสที่ผลิตภัณฑ์ ของบริษัทของเขาเคยเป็นที่ยอมรับของมหาชนเป็นเท่าใด" หรือ "โอกาสที่แต่ละบุคคลจะมีอายุถึง 100 ปีเป็นเท่าใด" ในการตอบคำถามดังกล่าวจำเป็นต้องใช้ความถี่ที่อาจจะเกิดขึ้น ซึ่งคำนวณได้ โดยพิจารณาจากการสังเกตการณ์ ของเหตุการณ์หนึ่ง ซึ่งปรากฏบ่อยครั้ง เช่น

จากการสำรวจนิสิตเข้ามหาวิทยาลัย 1,000 คน ปรากฏว่า 950 คนสำเร็จ ปริญญาตรี ความน่าจะเป็นของนิสิตที่เข้ามหาวิทยาลัย จะสำเร็จปริญญาตรีเป็น  950/1,000 = 0.95 

นอกจากนี้ความน่าจะเป็นอาจคำนวณโดยอาศัยดุลพินิจซึ่งขึ้นอยู่กับความเชื่อถือ ประสบการณ์ หรือ ความรู้สึกของบุคคล ที่ประมาณค่าของความน่าจะเป็น การคำนวณความน่าจะเป็นชนิดนี้ต้องพิจารณาถึงประจักษ์พยานที่เคยเกิดขึ้น ประจักษ์พยานที่เกิดขึ้นอาจจะเป็นปรากฏการณ์ หรือ การเดาที่ดี เช่น ความน่าจะเป็นที่ผลิตภัณฑ์ของบริษัทจะจำหน่ายได้มากขึ้น เป็นต้น 

ตัวแปรสุ่มเป็นจำนวนมาก มีลักษณะไม่ต่อเนื่องโดยธรรมชาติ ตัวแปรสุ่มไม่ต่อเนื่อง เป็นค่าที่แตกต่างจากกัน และ กัน ด้วยจำนวนที่นับได้ อีกนัยหนึ่ง ตัวแปรสุ่มไม่ต่อเนื่อง พิจารณาได้จากจำนวนของค่าต่างๆ หรือ จุดตัวอย่างที่นับได้ หรือ ค่าที่มีจำนวนสามารถนับได้ เช่น โยนเหรียญ 4 เหรียญ เราจะได้ปรากฏการณ์ ที่เกี่ยวกับหัวซึ่งอาจเกิดขึ้นได้เป็น 5 อย่าง คือ 0 1 2 3 4 จำนวนหัว หรือ ก้อยที่สังเกตได้นี้เป็นจำนวนเต็ม ตัวแปรสุ่มที่ต่อเนื่อง มีลักษณะเป็นค่าที่แตกต่างจากกัน ด้วยจำนวนที่เล็กมากจนนับไม่ถ้วน ได้แก่ ระยะทาง น้ำหนัก ฯลฯ การแจกแจงของตัวแปรสุ่มไม่ต่อเนื่องมีหลายลักษณะ เช่น การแจกแจงทวินาม (Binomial distribution) การแจกแจงไฮเพอร์จีออเมตริก (Hypergeometric distribution) และ การแจกแจงปัวส์ซงเอกซ์โพเนนเชียล (Poisson exponential distribution)

 

 

 

สมมุติว่าหยิบของจากกล่องที่มีของรวมอยู่ 100 ชิ้น และ มีของเสียปนอยู่ 5 ชิ้น โดยให้หยิบขึ้นมาชิ้นหนึ่ง ทดสอบว่า ดี หรือ เสีย แล้วคืนลงกล่องตามเดิมคนให้เข้ากันแล้วหยิบใหม่ ทำเช่นนี้ 3 ครั้ง ตามทฤษฎี จะบอกได้ล่วงหน้าว่า โอกาสที่จะไม่พบของเสียเลย หรือ พบของเสีย 1 ชิ้น หรือ 2 ชิ้น หรือ เสียทั้ง 3 ชิ้นมีเพียงใดโดยคำนวณจากสูตร 

 

 

 

เมื่อ n คือ จำนวนของที่หยิบทั้งหมด

 

x คือ จำนวนของเสียที่จะได้ใน n มีค่าได้ตั้งแต่ 0 ถึง n

 

p คือ ค่าของความน่าจะเป็นที่จะได้ของเสีย ในการหยิบแต่ละครั้ง ซึ่งเป็นค่าคงที่

 

q คือ 1 - p

 

n! คือ ผลคูณ n (n-1) (n-2)...3.2.1

ในที่นี้ n = 3

 

x = 0 หมายถึงใน 3 ชิ้นที่หยิบไม่มีของเสียเลย

 

x = 1 หมายถึงใน 3 ชิ้นที่หยิบจะพบของเสีย 1 ชิ้น ซึ่งอาจจะเป็นชิ้นแรกที่หยิบ หรือ ชิ้นที่ 2 หรือ ชิ้นที่ 3 ก็ได้

 

x = 2 หมายถึงใน 3 ชิ้นที่หยิบจะพบของเสีย 2 ชิ้น ซึ่งอาจจะเป็นชิ้นที่ 1 กับชิ้นที่ 2 หรือ ชิ้นที่ 2 หรือ ชิ้นที่ 1 กับ ชิ้นที่ 3 หรือ ชิ้นที่ 2 กับชิ้นที่ 3

 

x = 3 หมายถึงใน 3 ชิ้นที่หยิบจะพบของเสียทั้ง 3 ชิ้น

 

ค่า p ในตัวอย่างนี้คือ 5 = 1 ซึ่งเป็นค่าคงที่ไม่ว่าจะ 100 20 หยิบครั้งใดๆ เพราะได้มีการคืนของที่หยิบลงกล่องตามเดิม และ ทำให้โอกาสที่จะหยิบชิ้นใดขึ้นมาใหม่มีเท่ากันเหมือนเดิม

โดยการแทนค่าในสูตร (1) จะได้ความน่าจะเป็นของการได้ x = 0, 1, 2, 3, ซึ่งจะใช้สัญลักษณ์ P(x) ดังนี้ 

 

 

 

สังเกตได้ว่า ถ้าหยิบของ 3 ชิ้น จากกล่องที่มีของเสีย 5 เปอร์ เซ็นต์ เรามักจะไม่พบของเสีย เพราะ โอกาสที่จะไม่พบของเสีย คือ โอกาสที่ x = 0 มีค่าถึง 0.86 หรือ 86 เปอร์เซ็นต์ โอกาสที่จะพบของเสีย 1 ชิ้น มีเพียง 0.13 หรือ 13 เปอร์เซ็นต์ และ โอกาสที่จะพบของเสีย 2 ชิ้น มีเพียง 1 เปอร์เซ็นต์ ส่วนที่จะพบของเสียทั้ง 3 ชิ้น นั้นน้อยมากเกือบไม่มีเลย
จากค่าของความน่าจะเป็นนี้ จะทำให้ทราบจำนวนของเสียโดยเฉลี่ย หรือ โดยประมาณจากสูตร

 

จำนวนของเสียโดยเฉลี่ยที่หยิบได้ในการหยิบ n ชิ้น คือ np

สมมุติว่า หยิบของ 20 ชิ้น จากกล่องดังกล่าวแล้ว หมายความว่า n=20, p=1/20 ฉะนั้น จะพบของเสียประมาณ 1 ชิ้น โดยคำนวณจาก np20(1/20) =1

สูตร (1) เป็นสูตรที่ให้ค่าความน่าจะเป็นที่สำคัญ และ มีชื่อว่า "การแจก แจงทวินาม" เพราะ จะแจกแจงค่าของความน่าจะเป็นของเหตุการณ์ที่จะปรากฏได้ 2 ลักษณะ เช่น ของเสีย หรือ ของไม่เสียตามตัวอย่าง โดยทั่วไปถ้าเรียกลักษณะที่สนใจว่า "สำเร็จ" และ เรียกลักษณะที่ไม่สนใจว่า "ไม่สำเร็จ" เช่น ถ้าสนใจว่า ในข้อสอบแบบปรนัย 100 ข้อ ที่ให้นักเรียนเลือกคำตอบที่ถูก 1 ข้อ จากบรรดาคำตอบ 4 ข้อของแต่ละคำถามนั้น จะมีที่ตอบถูก เพราะ เดาอย่างไรบ้าง ก็จะพิจารณาได้จากค่าของความน่าจะเป็น ของการที่นักเรียนจะตอบถูก เพราะ เดา ซึ่งแต่ละคำถามจะมีโอกาสถูกเพียง 1/4

รูปร่าง หรือ รูปแบบของการแจกแจงทวินาม ขึ้นอยู่กับค่า p และ n ถ้า p = q = 1 - p = 0.5 การแจกแจงจะสมมาตร โดยไม่คำนึงถึงค่า n ถ้า p ไม่เท่ากัน q การแจกแจง จะไม่สมมาตร กำหนดค่า n ให้ ถ้าค่า p และ q ต่างกันมากเท่าใดการแจก แจงจะเบี้ยวมากขึ้นเท่านั้น ถ้าค่า p ต่ำกว่าค่า q การแจกแจงจะเบี้ยวไปทางขวา หรือเรียกว่า เบี้ยวบวก เมื่อค่า p มากกว่าค่า q การแจกแจงจะเบี้ยวไปทางซ้าย หรือเรียกว่าเบี้ยวลบ อย่างไรก็ดีเมื่อค่าของ n มากขึ้น การแจกแจงจะเริ่มเบี้ยว น้อยลง เมื่อ n มีค่าใกล้อนันต์ การแจกแจงจะยิ่งสมมาตรมากขึ้น โดยไม่คำนึง ถึงค่าแตกต่างระหว่าง p และ q 

 

 

 

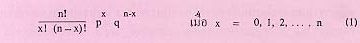
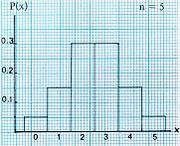
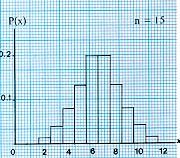
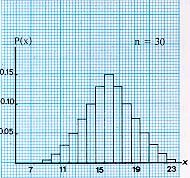
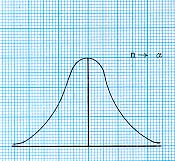
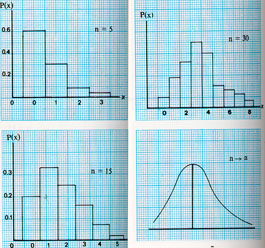
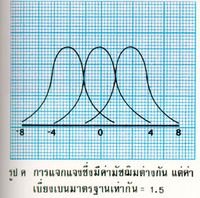
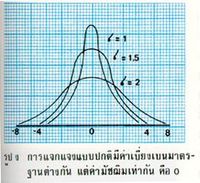
รูป ข ลากขึ้น โดยมีข้อสมมุติที่ว่า ความน่าจะเป็นของการสำเร็จ ในการทดลองหนึ่งครั้ง เป็น 0.1 เช่น การทดลองการหยิบ 0 จากตารางตัวเลขสุ่ม แสดงให้เห็นว่า เมื่อ n มีค่าใกล้อนันต์ หรือ เมื่อค่า n เพิ่ม การแจกแจงทวินามจะกลายเป็นเส้นโค้งต่อเนื่องสมมาตร ไม่ว่า p และ q จะเท่ากันหรือไม่ การแจกแจงรูปโค้งระฆังคว่ำที่ต่อเนื่องเช่นนี้ คือ การแจกแจงปกติ ซึ่งเป็นขีดจำกัดของการแจกแจงทวินาม เมื่อ n มีค่าใกล้อนันต์

การแจกแจงทวินามขึ้นอยู่กับข้อสมมุติที่ว่า ประชากรนั้นมีมากจนนับไม่ได้ และ ตัวอย่างสุ่มนั้นเลือกมาโดยวิธีนำไปแทนที่ กล่าวคือ จะต้องคืนหน่วยที่หยิบขึ้นมาสังเกตแล้วลงไปก่อนที่จะมีการหยิบหน่วยต่อไป ดังนั้นการสังเกตการณ์จึงเป็นอิสระแก่กัน ความน่าจะเป็นของการสังเกตการณ์ในแต่ละครั้งจะไม่เปลี่ยนแปลง แต่ถ้าประชากรนับได้ และ ตัวอย่างสุ่มออกมา โดยวิธีไม่นำไปแทนที่ คือ เมื่อหยิบหน่วยขึ้นมาสังเกตแล้วไม่คืนลงไปที่เดิมก่อนที่จะหยิบหน่วยต่อไป ความน่าจะเป็นจะเปลี่ยนไป สำหรับการสังเกตการณ์แต่ละครั้ง การแจกแจงความน่าจะเป็นในกรณีนี้เรียกว่า การแจกแจงไฮเพอร์จีออเมตริก

ถ้าหยิบของ n หน่วย โดยวิธีไม่นำไปแทนที่จากเซตหนึ่งซึ่งประกอบด้วย ของชนิดหนึ่งจำนวน N1 หน่วย และ อีกชนิดหนึ่งจำนวน N2 หน่วย ทั้ง 2 ชนิด นี้เกิดขึ้นพร้อมกันไม่ได้ ดังนั้น จำนวนทางทั้งหมดในการหยิบของ n หน่วย จาก ประชากรนี้ คือ

 

 

แสดงว่าในหนังสือเล่มนั้น จะมีคำผิดหน้าละ 5 คำอยู่ประมาณ 10 เปอร์เซ็นต์ หมายความว่าถ้าหนังสือหนา 100 หน้า จะมีคำผิดหน้าละ 5 คำอยู่ประมาณ 10 หน้า แต่บอกไม่ได้ว่าหน้าไหน

 

 

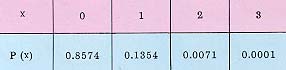
อีกตัวอย่างหนึ่ง สมมุติว่า เครื่องจักรอัตโนมัติผลิตสกรูออกมาแล้ว มีสกรูที่ใช้ไม่ได้หรือเสีย จำนวน 2 เปอร์เซ็นต์ เครื่องมือที่ยังไม่ได้ประกอบชนิดหนึ่ง ต้องการสกรู 98 ตัว สำหรับประกอบ และ สกรูนี้จะจัดอยู่ในกล่องๆ ละ 100 ตัว ความน่าจะเป็นที่ผู้ซื้อเครื่องมือชนิดนี้ จะไม่มีสกรูที่ดีเพียงพอ ที่จะประกอบให้ สำเร็จได้ สำหรับ m = np = 100 (.02) = 2 ซึ่งสามารถคำนวณจากความน่า จะเป็นที่จะได้สกรูเสีย 0, 1 หรือ 2 หน่วย คือ 

 

ดังได้กล่าวแล้วว่าการแจกแจงทวินาม จะมีค่าใกล้การแจกแจงต่อเนื่อง ของรูปที่สมมาตร ถ้า n เพิ่มขึ้นให้มากพอ การแจกแจงที่สมมาตรนี้จะใกล้เคียง กับการแจกแจงปกติซึ่งเป็นขีดจำกัดของการแจกแจงทวินาม สิ่งที่น่าสนใจ คือ การแจกแจงปกติก็เป็นขีดจำกัดของการแจกแจงปัวส์ซงด้วย กำหนดค่าของ p ให้ np จะเพิ่มขึ้นอีกเมื่อ n เพิ่มขึ้น กราฟของการแจกแจงปัวส์ซงจะมีลักษณะใกล้กับโค้งรูประฆังคว่ำมากขึ้นทุกที 

เส้นโค้งเรียบรูประฆังคว่ำที่แสดงในรูป ก หรือ รูป ข เรียกว่าเส้นโค้งปกติ ซึ่งเป็นขีดจำกัดของการแจกแจงทวินามเมื่อ n มีค่าใกล้อนันต์ เราได้ทราบฟังก์ชัน ความน่าจะเป็นทวินาม ดังนี้ 

 

 

สมมุติว่าโรงงานผลิตหลอดไฟแห่งหนึ่ง เก็บข้อมูลเกี่ยวกับอายุของหลอด ไฟไว้ และ คำนวณได้ว่าโดยเฉลี่ยแล้วหลอดหนึ่งๆ จะมีอายุ 800 ชั่วโมง คือนับ ตั้งแต่เริ่มใช้จนกระทั่งหลอดเสียจะใช้เวลาประมาณ 800 ชั่วโมง และ ส่วนเบี่ยงเบนมาตรฐาน 40 ชั่วโมง ถ้าทราบหรือทดสอบไว้ว่าอายุหลอดไฟมีการแจกแจงปกติ ก็จะสามารถคำนวณความน่าจะเป็นที่หลอดไฟจะมีอายุเท่าใดได้ เช่น ความน่าจะเป็น หรือ โอกาสที่จะพบหลอดไฟซึ่งใช้ได้นานระหว่าง 778 ถึง 834 ชั่วโมง จะคำนวณได้จากสูตร (3) ซึ่งจะให้ค่า 0.51 นั่นคือ จะมีหลอดไฟเหล่านี้ ประมาณ 51 เปอร์เซ็นต์ ที่มีอายุระหว่าง 778 ถึง 834 ชั่วโมง

 

 

สูตร (1), (3) และ (4) ที่ใช้ในการหาค่าของความน่าจะเป็นของเรื่อง ที่แทนได้ด้วย x นั้น จะมีคำนวณไว้ให้ในตารางของหนังสือเรื่องความน่าจะเป็นทั่วๆ ไป นอกจากการแจกแจงความน่าจะเป็นขั้นพื้นฐานที่สำคัญ ทั้งสามแบบนี้แล้ว ยังมีแบบต่างๆ อีกมากที่สลับซับซ้อน และ ยุ่งยากมากขึ้น ต่างก็มีลักษณะ เฉพาะสำหรับเหตุการณ์ที่จะเกิดขึ้น ซึ่งสามารถใช้ความรู้ทางสถิติทดสอบได้ว่า เหตุการณ์ที่คาดว่าจะมีความน่าจะเป็นตามที่คาดคะเนนั้น จะมีการกระจายของ ความน่าจะเป็นตามที่ตั้งรูปแบบไว้ หรือ ไม่ ในชั้นสูงขึ้นไปจะได้เห็นความสัมพันธ์ ระหว่างคณิตศาสตร์ชั้นสูง และ เรื่องราวของความน่าจะเป็นมากขึ้น ในระยะประมาณ 40 ปีที่ผ่านมานี้ ความน่าจะเป็นได้รับความสนใจ และ การนำไปใช้ในทางวิทยาการอย่างมาก ผิดกับในสมัยเริ่มแรกที่วิชานี้ได้มีกำเนิดขึ้น