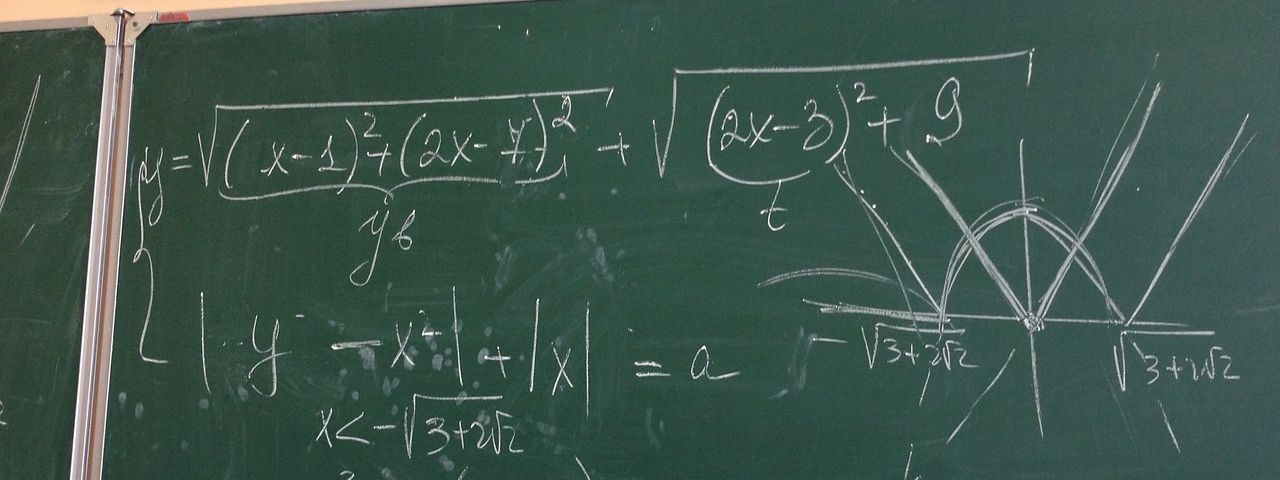
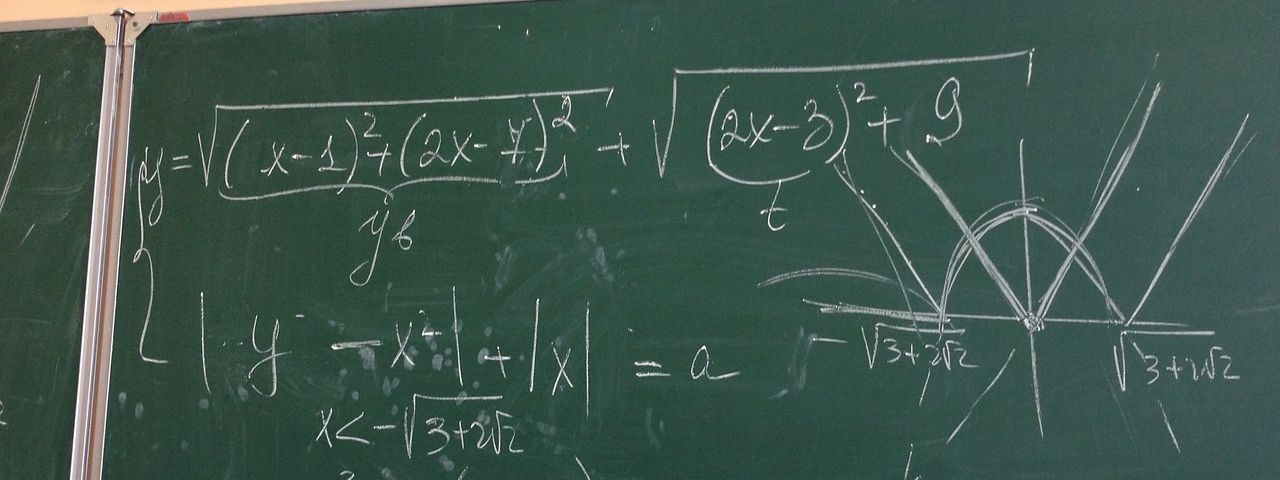
 3,526 Views
3,526 Views
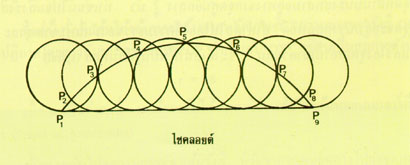
ถ้าเราทำเครื่องหมายไว้แห่งหนึ่งบนขอบนอกของล้อรถ เช่น ล้อรถจักรยาน เมื่อรถวิ่งไปบนพื้นราบ เราจะสังเกตเห็นว่าเครื่องหมายที่ทำไว้นั้น ก็จะเคลื่อนที่ไปด้วยเมื่อตรวจสอบทางเดินของเครื่องหมายที่ทำไว้จะเห็นว่า เป็นเส้นโค้งชนิดหนึ่ง ในทางคณิตศาสตร์เรียกเส้นโค้งนี้ว่า ไซคลอยด์ (cycloid) มีลักษณะคล้ายคลื่น ฉะนั้นไซคลอยด์ก็คือทางเดินของจุดๆ หนึ่งบนวงกลมที่กลิ้งไปบนเส้นตรง
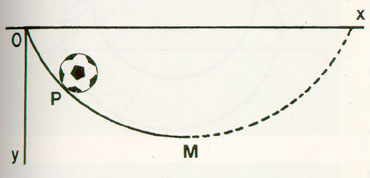
ถ้าหงายเส้นโค้งไซคลอยด์ลง และ ให้ M เป็นจุดต่ำที่สุดของเส้นโค้งนี้ คุณสมบัติพิเศษของไซคลอยด์ก็คือ เมื่อเอาลูกบอลวางไว้ที่จุด P ซึ่งอยู่ที่ส่วนใดๆ ของเส้นโค้งนี้ก็ตาม เมื่อปล่อยลูกบอลให้กลิ้งลงมาตามเส้นโค้ง ลูกบอล จะมาถึงจุด M ในเวลาเท่ากันหมด
ท่านอาจจะลองคิดต่อไปว่า ถ้า P1 เป็นจุดๆ หนึ่งบนรัศมี OP เมื่อวงกลมกลิ้งไปบนเส้นตรงทางเดินของจุด P1 จะมีลักษณะอย่างไร ถ้า P2 เป็นจุดๆ หนึ่งบนรัศมี OP ที่ต่อออกไปทางเดินของจุด P2 จะเป็นอย่างไรเมื่อกลิ้งวงกลมไปบนเส้นตรง
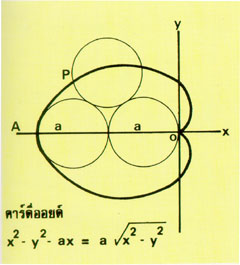
ทดลองโดยเอาเหรียญบาทมาสองอัน วางเหรียญหนึ่งไว้ให้อยู่กับที่ทำเครื่องหมายไว้หนึ่งแห่งที่ขอบของเหรียญที่สองแล้วค่อยๆ กลิ้งเหรียญที่สองรอบเหรียญที่วางไว้อยู่กับที่จนรอบ ทางเดินของเครื่องหมายบนขอบเหรียญที่สอง จะเป็นเส้นโค้งมีลักษณะ (ดังรูป) ดูคล้ายกับรูปหัวใจ ทางคณิตศาสตร์เรียกเส้น โค้งชนิดนี้ว่า คาร์ดีออยด์ (cardioid) ซึ่งเป็นทางเดินของจุดๆ หนึ่งบนวงกลมที่กลิ้งรอบวงกลมที่อยู่กับที่อีกวงหนึ่ง
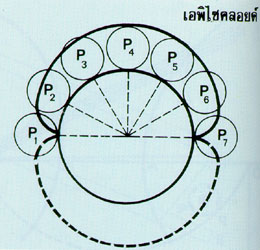
คราวนี้ลองให้วงกลมที่กลิ้งไปนั้น มีรัศมีน้อยกว่ารัศมีของวงกลมที่อยู่กับที่ จุดที่ทำเครื่องหมายบนวงกลมวงนอกจะอยู่บนวงกลมวงในมากกว่าหนึ่งแห่งทำให้ทางเดินเป็นส่วนโค้ง (arch) มากกว่าหนึ่งส่วน เช่น ถ้าวงกลมวงนอกมีรัศมี เท่ากับครึ่งหนึ่งของรัศมีของวงกลมวงใน จะได้เส้นโค้งเป็นส่วนโค้งสองส่วน ถ้าวงกลมวงนอกมีรัศมีเพียงเศษหนึ่งส่วน n ของรัศมีวงกลมวงใน ก็จะได้ส่วนโค้ง n ส่วนรอบวงกลมวงใน เราเรียกเส้นโค้งชนิดนี้ว่า เอพิไซคลอยด์ (Epicycloid) เส้นโค้งคาร์ดิออยด์เป็นกรณีเฉพาะของเส้นโค้งเอพิไซคลอยด์
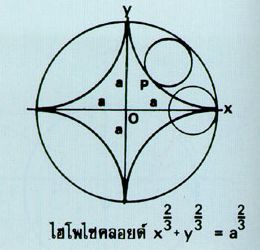
ถ้าเอาวงกลมเล็กไปกลิ้งภายในวงกลมใหญ่ซึ่งอยู่กับที่ จุดที่อยู่บนวงกลมเล็กจุดหนึ่งก็จะขีดเส้นโค้งขึ้นภายในวงกลมใหญ่ เราเรียกทางเดินของจุดเช่นนี้ว่า ไฮโพไซคลอยด์ (Hypocycloid) จำนวนเส้นโค้งภายในวงกลมใหญ่จะมี n ส่วนโค้ง เมื่อวงกลมใหญ่มีรัศมีเป็น n เท่าของรัศมีวงกลมเล็ก
ท่านอาจจะลองเขียนเส้นโค้งไฮโพไซคลอยด์ เมื่อวงกลมใหญ่มีรัศมีเป็นสองเท่า และ สามเท่าของวงกลมเล็กดูบ้างว่าเส้นโค้งมีลักษณะอย่างไร การเขียนเส้นโค้งโดยใช้เส้นรังสี และ มุมเขียนวงกลมรัศมี 2 1/4 นิ้ว จากจุดศูนย์กลางเขียนเส้นรังสี 18 เส้นให้ทำมุมเท่ากับ 20 องศาเท่าๆ กันโดยใช้ไม้โพรแทรกเตอร์ (ไม้ที่มีสเกลแบ่งมุม) ให้ตัวเลขรังสีเริ่มจาก 0 ถึง 17 แล้วต่อไปเป็น 18, 19, 20,...ตามรูป กำหนดจุดบนเส้นรังสีเหล่านี้ จุดแรกบนรังสีที่หนึ่งอยู่ห่างจากจุดศูนย์กลาง 1/8 นิ้ว จุดที่สองบนรังสีที่สองอยู่ห่างจากจุดศูนย์กลาง 2/8 นิ้ว จุดที่สามบนรังสีที่สามอยู่ห่างจากจุดศูนย์กลาง 3/8 นิ้ว ทำเช่นนี้ไปจนถึงรังสีที่ 18 จุดจะอยู่บนวงกลมพอดี ถ้าทำต่อไปโดยให้ความยาวของรังสีเพิ่มขึ้นครั้งละ 1/8 นิ้ว แล้วโยงจุดเหล่านี้เข้าด้วยกัน จะได้เส้นโค้งเป็น รูปก้นหอย (spiral)

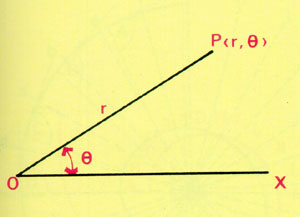
จุดต่างๆ บนเส้นโค้งก้นหอยสร้างจากหลักเกณฑ์ "ความยาวของรังสี OP เป็นปฏิภาคโดยตรงกับขนาดของมุมที่ OP ทำกับเส้น OX" เขียนเป็นสมการดังนี้
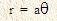
เมื่อ a เป็นค่าคงที่ เราเรียกเส้นโค้งแบบนี้ว่า เส้นโค้งก้นหอยแบบอาร์คีมีดีส (Spiral of Archimedes)
ถ้าลองกลับไปดูความยาวของเส้นรังสีที่วัดจากจุดศูนย์กลางไปยังจุดบน เส้นโค้งก้นหอยแบบอาร์คีมีดีส จะเห็นว่าความยาวจะเพิ่มขึ้นเป็นความก้าวหน้า เลขคณิต ดังนี้
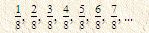
เราอาจจะสร้างเส้นโค้งก้นหอยอีกแบบหนึ่ง ให้ความยาวของรังสีค่อยๆ เพิ่มขึ้นแบบความก้าวหน้าเรขาคณิตก็ได้เมื่อมุมของรังสีเท่ากันหมดที่จุดศูนย์ กลาง เส้นโค้งก้นหอยที่น่าสนใจแบบหนึ่งมีความยาวของรังสีที่อยู่ห่างกัน 12 พจน์ เป็น 2 เท่ากัน กล่าวคือ ถ้าความยาวของรังสีเรียงตามลำดับแบบความก้าวหน้า เรขาคณิต
r, r^2, r^3,...r^n,...
เมื่อแทนรังสีที่ n ด้วย rn ดังนั้น rn = r^n จะได้
ดังนั้น
แบ่งมุมรอบจุด O ออกเป็น 24 ส่วนเท่าๆ กันโดยเส้นรังสี Oa, Ob, Oc, B, C,...บนเส้นรังสี Oa, Ob, Oc,...ดังต่อไปนี้
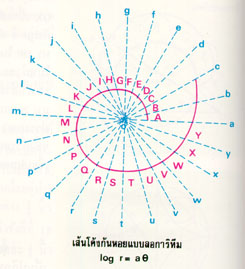
จุด A อยู่บน Oa ให้ OA = 1.00 หน่วย
B " Ob " OB = 1.06 "
C " Oc " OC = 1.12 "
D " Od " OD = 1.19 "
E " Oe " OE = 1.26 "
F " Of " OF = 1.33 "
G " Og " OG = 1.41 "
H " Oh " OH = 1.50 "
I " Oi " OI = 1.59 "
J " Oj " OJ = 1.68 "
K " Ok " OK = 1.78 "
L " Ol " OL = 1.89 "
M " Om " OM = 2.00 "
N " On " ON = 2.12 "
P " Op " OP = 2.24 "
Q " Oq " OQ = 2.38 "
R " Or " OR = 2.52 "
S " Os " OS = 2.66 "
T " Ot " OT = 2.83 "
U " Ou " OU = 3.00 "
V " Ov " OV = 3.17 "
W " Ow " OW = 3.36 "
X " Ox " OX = 3.56 "
Y " Oy " OY = 3.77 "
A' " Oa " OA' = 4.00 "
B' " Ob " OB' = 4.24 "
C' " Oc " OC' = 4.49 "
จากการสังเกตจะเห็นว่า
OA' = 4 OA
OB' = 4 OB
OC' = 4 OC
...................
OA" = 4 OA' = 16 OA
OB" = 4 OB' = 16 OB
OC" = 4 OC' = 16 OC
เส้นโค้งก้นหอยแบบนี้มีคุณสมบัติพิเศษประการหนึ่งคือ เส้นรังสี และ เส้นสัมผัสกับเส้นโค้งจะทำมุมเท่ากันหมดตลอดทุกจุดบนเส้นโค้ง นักคณิตศาสตร์เรียก เส้นโค้งแบบนี้ว่า เส้นโค้งก้นหอยแบบมีมุมเท่ากัน (equiangular spiral) หรือเรียกว่า เส้นโค้งก้นหอยแบบลอการิทึม (logarithmic sprial) และ มีสมการทางคณิต ศาสตร์ ดังนี้

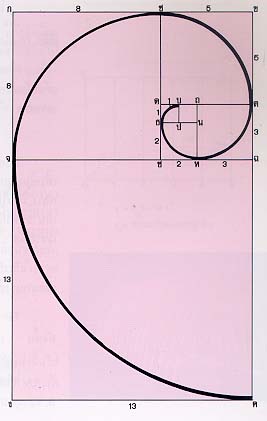
ท่านอาจจะเขียนเส้นโค้งแบบก้นหอยแบบมีมุมเท่ากัน โดยใช้ไม้บรรทัด และ วงเวียนเท่านั้นก็ได้ โดยดำเนินการตามลำดับดังนี้
ส่วนโค้งของวงกลมที่เริ่มต้นจากจุด ค ไปจนถึงจุด บ จะเป็นเส้นโค้งก้น หอยแบบมีมุมเท่ากัน
จากวิธีการนี้จะเห็นได้ว่าเรามีรูปสี่เหลี่ยมจัตุรัส ที่มีความยาวของแต่ละ ด้านเรียงกันดังนี้
1, 1, 2, 3, 5, 8, 13,...
แต่ละพจน์ของอันดับนี้ ได้จากผลบวกของสองพจน์ ซึ่งอยู่ข้างหน้าติด กับพจน์นั้นมาบวกกัน เช่น
2 = 1+1, 3 = 1+2, 5 = 2+3, 8 = 3+5, 13 = 5+8, 21 =8+13
โดยหลักเกณฑ์นี้ เราก็จะเขียนพจน์ต่อไปได้เรื่อยๆ ไม่สิ้นสุด นักคณิต ศาสตร์เรียกจำนวนที่เรียงกันไปตามกฎเกณฑ์เช่นนี้ว่า อันดับฟิโบนักชี (Fibonacci sequence) ของจำนวน จากความรู้ที่ได้นี้ ท่านจะเขียนเส้นโค้งก้นหอยให้มีขนาดใหญ่ขึ้น โดยสร้างจัตุรัส ที่มีความยาวของแต่ละด้านเป็นเลขในอันดับฟิโบนักชีต่อไปได้เรื่อยๆ

ในธรรมชาติ เราอาจจะสังเกตเห็นลวดลายของหอยหลายชนิด ลวดลายของดอกไม้บางประเภท และ ลวดลายของตาสับปะรด เป็นต้น มีลักษณะคล้ายกับเส้นโค้งก้นหอยสองชุดตัดกัน

กระดาษกราฟที่จะใช้สำหรับวิธีที่จะกล่าวนี้มีลักษณะเป็นวงกลมที่มีจุดศูนย์กลางร่วมกันหลายๆ วง และ เส้นรังสีที่ออกจากจุดศูนย์กลางทำมุมขนาดต่างๆ กัน เราเรียกกระดาษกราฟแบบนี้ว่า กระดาษกราฟโพลาร์ (Polar graph)


วิธีเขียนเส้นโค้งโดยวัดความยาวของรังสีจากจุดคงที่จุดหนึ่ง และ มุมที่รังสีกระทำเส้นตรงคงที่เส้นหนึ่งนี้ เป็นวิธีที่นักวิทยาศาสตร์สามารถตรวจสอบได้ว่า ทางเดินของดวงดาวต่างๆ ตลอดจนทางเดินของดาวบริวารที่มนุษย์ประดิษฐ์ขึ้น จะมีลักษณะเป็นเส้นโค้งแบบไหน และ สามารถบอกตำแหน่งได้ทุกเวลาด้วย
