ไฮเพอร์โบลา (Hyperbola)

มีจุดคงที่หรือจุดโฟกัสสองจุดเช่นเดียวกับวงรี ถ้าเราให้จุดๆ หนึ่งเคลื่อนที่ไปโดยมีผลต่างของระยะทางระหว่างจุดที่เคลื่อนที่ และ จุดคงที่ทั้งสองมีค่าคงที่แล้ว จุดที่เคลื่อนที่ไปนั้นจะขีดรอยเส้นโค้งขึ้นซึ่งเรียกว่า เส้นโค้งไฮเพอร์โบลา และ จะมีเส้นโค้งเช่นนี้ถึงสองส่วนโดยไม่ติดต่อกันเลย 

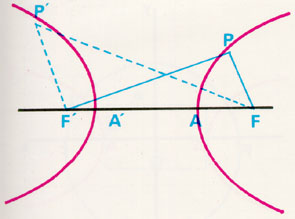
ตามรูป F และ F' เป็นจุดคงที่สองจุด P เป็นจุดที่กำลังเคลื่อนที่โดยมี คุณสมบัติว่า PF'- PF = ค่าคงที่ = K ทางเดินของจุด P จะเป็นส่วนหนึ่งของเส้นโค้งไฮเพอร์โบลา แต่ถ้าเราให้ P' เป็นจุดที่กำลังเคลื่อนที่โดยมีคุณสมบัติว่า P'F - P'F' = ค่าคงที่ = K ทางเดินของจุด P ก็จะเป็นอีกส่วนหนึ่งของไฮเพอร์โบลาเดียวกัน

ถ้าลากเส้นตรงผ่าน F และ F' เส้นตรงนี้จะตัดส่วนทั้งสองของเส้นโค้ง ไฮเพอร์โบลาที่ A และ A' ซึ่งเราเรียกว่าจุดยอดของเส้นโค้ง เนื่องด้วย A และ A' ต่างก็อยู่บนเส้นโค้ง ดังนั้น AF'- AF = K = A'F - A'F'
จุด A และ A' ต่างก็เป็นจุดที่ และ AF = A'F' ดังนั้น K = AA' เท่ากับระยะห่างระหว่างจุดยอดทั้งสองของไฮเพอร์โบลา แสดงว่าผลต่างของระยะทางจากจุดโฟกัสไปยังจุดบนไฮเพอร์โบลานั้น เท่ากับระยะห่างระหว่างจุดยอดทั้งสองของไฮเพอร์โบลา

เราอาจจะเขียนเส้นโค้งไฮเพอร์โบลาด้วยไม้บรรทัด เส้นด้าย และ ดินสอ ดังนี้ กำหนดจุดคงที่ F และ F' ไว้บนกระดาษ ใช้เส้นด้ายที่มีความยาวน้อยกว่า ความยาวของไม้บรรทัด และ ให้ผลต่างของความยาวของไม้บรรทัด และ เส้นด้ายน้อยกว่าระยะทาง ระหว่าง F และ F' พอสมควร ใช้หมุดตรึงปลายข้างหนึ่งของไม้บรรทัดไว้ที่จุด F' ผูกปลายหนึ่งของเส้นด้ายไว้ที่จุด F และ ผูกอีกปลายหนึ่งไว้ที่ปลายอีกข้างหนึ่ง (ในรูปคือจุด B) ใช้ปลายดินสอดึงเส้นด้ายให้ตึง โดยให้เส้นด้ายส่วนหนึ่ง อยู่ในแนวของไม้บรรทัดที่ค่อยๆ หมุนไป ปลายดินสอก็จะขีดรอยเส้นโค้งไฮเพอร์โบลาส่วนหนึ่งซึ่งอยู่เหนือเส้น FF' การเขียนส่วนโค้งส่วนที่อยู่ใต้ FF' ก็เพียงแต่วางไม้บรรทัดตามเส้นประ (ดังในรูป)

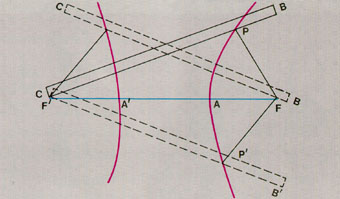
การเขียนส่วนที่สองของเส้นโค้งก็เปลี่ยนเอาปลายไม้บรรทัดอีกปลายหนึ่งให้หมุนรอบจุด F เอาเส้นด้ายผูกปลายไว้ที่ C และ F' และ กระทำเช่นเดียวกันก็จะได้เส้นโค้งส่วนที่สอง

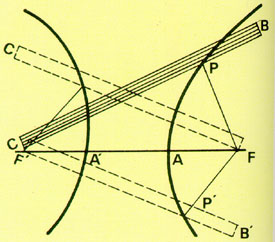
จากรูป PF' - PF = (PF'+ PB) - (PF + PB)
                            = CB - (PF + PB)
                            = ความยาวของไม้บรรทัดความยาวของด้าย 
                            = ความยาวคงที่จำนวนหนึ่ง 
                            = ระยะทางระหว่าง A และ A'

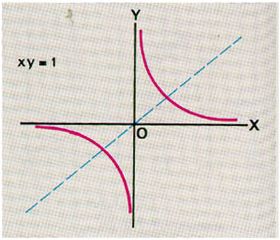
สมการทั่วไปของเส้นโค้งไฮเพอร์โบลามีแบบเป็น  x^2/a^2 - y^2/b^2 = 1