

 1,299 Views
1,299 Views
เราได้ความรู้จากนักปราชญ์ชาวกรีกสมัยโบราณ เมื่อประมาณ ๖๐๐ ปีก่อนคริสต์ศักราชว่าโลกเรามีสัณฐานทรงกลมแต่ก็ยังไม่มีใครคำนวณได้ดีจนถึงเมื่อประมาณ ๒๔๐ ปี ก่อนคริสต์ศักราชนักปราชญ์ชาวกรีกผู้ยิ่งใหญ่ชื่อ เอราโทรเทเนส (Eratosthenes, ประมาณ ๒๗๖ - ๑๙๔ ปี ก่อนคริสต์ศักราช, ชาวกรีก, นักคณิตศาสตร์) ได้วัดขนาดของโลกว่ามีเส้นรอบวงยาว ๔๐,๐๐๐ กิโลเมตร
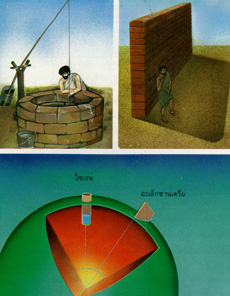
เอราโทสเทเนส ผู้วัดขนาดโลกเมื่อ ๒๔๐ ปีก่อนคริสต์ศักราชก่อนที่ แมเกลแลน เดินทางทางเรือไปรอบโลก ๑,๗๐๐ ปี พบว่าเมื่อดวงอาทิตย์อยู่เหนือสุดประมาณ ๒๑-๒๒ มิถุนายน ที่อะเล็กซานเดรียแสงอาทิตย์ส่องตรงในบ่อน้ำที่ไซเอนเมื่อแสงอาทิตย์ส่องที่อะเล็กซานเดรียซึ่งอยู่ห่างจากไซเอนประมาณ ๘๐๐ กิโลเมตร เงาเสาเอนประมาณ๗.๒ องศา เขาคำนวณมุมศูนย์กลางโลกระหว่างไซเอน และ อะเล็กซานเดรีย เท่ากับ ๑/๕๐ ของ ๓๖๐ องศา ได้เส้นรอบวงของโลก ๕๐ เท่า ระยะระหว่างไซเอน และ อะเล็กซานเดรียเท่ากับ ๔๐,๐๐๐ กิโลเมตร
เอราโทสเทเนสได้สังเกตการเคลื่อนที่ของดวงอาทิตย์พบว่าดวงอาทิตย์เวลาเที่ยงวันในฤดูร้อนเมื่อวันที่ดวงอาทิตย์อยู่ทางด้านเหนือเส้นศูนย์สูตรท้องฟ้าเหนือที่สุดได้ส่องแสงตรงลงมาเห็นเงาอยู่ใน บ่อ ๆ หนึ่งที่ไซเอน (Syene) ปัจจุบันนี้เรียกว่า อาสวาน (Aswan) เขาทราบว่าขณะเดียวกับที่อะเล็กซานเดรีย (Alexandria) ซึ่งอยู่ทางเหนือไซเอนขึ้นไป ประมาณ ๘๐๐ กิโลเมตร ดวงอาทิตย์ทำเงาเอียง วัดได้ ๗.๒ องศา หรือประมาณ ๑/๕๐ ของ ๓๖๐ degree เขาจึงคำนวณได้รอบวงของโลกเป็น ๕๐x๘๐๐ หรือ ๔๐,๐๐๐ กิโลเมตร ขนาดจริงของโลกที่วัดได้ด้วยเครื่องมือเครื่องใช้สมัยใหม่แตกต่างจากที่เอราโทสเทเนสวันได้ไม่ถึง ๑๖๐ กิโลเมตร
|
โดยที่โลกมีสัณฐานเป็นทรงกลม และ มีขนาดใหญ่โตมากจุดใดจุดหนึ่งบนทรงกลมมีลักษณะเหมือนจุดอื่น ๆ ไม่มีอะไรแตกต่างกันระบบการบอกตำแหน่งจุดมาจากเคลาดิอุส โตเลมี (Claudius Ptolemy ประมาณ ค.ศ. ๒๐๐, ชาวกรีก, นักคณิตศาสตร์) โตเลมีอยู่ในอียิปต์ทำงานเกี่ยวกับห้องสมุด และ สอนที่โรงเรียนในนครอะเล็กซานเดรียเป็นผู้ให้ความคิด และ ให้แบบอย่างไว้ในแผนที่ที่เขาได้รวบรวมทำขึ้นเขาแบ่งผิวโลกโดยใช้ระบบพิกัดทางเรขาคณิต ระบบพิกัดนี้ก็คือวงขนานละติจูดและวงเมริเดียนลองจิจูดใช้บอกตำแหน่งจุดทั้งบนบก และ ในทะเล วงขนาน ละติจูดเป็นวงขนานกับศูนย์สูตรของโลกส่วนวงขนานลองจิจูดเป็นวงซึ่งตั้งได้ฉากกับศูนย์สูตรโลกซึ่งไปรวมกันที่ขั้วโลก |
