นักปราชญ์ และนักดาราศาสตร์ยุคโบราณ มีความเชื่อในแบบจำลองของระบบสุริยะหลากหลายรูปแบบแตกต่างกัน ผู้ศึกษาดาราศาสตร์ตั้งแต่ยุคโบราณมามีอยู่หลายท่าน ตั้งแต่ อริสโตเติล, ทอเลมี, นิโคลัส โคเปอร์นิคัส, ไทโค บราห์ และโจฮันเนส เคปเลอร์ ผู้สร้างกฎการเคลื่อนที่ของดาวเคราะห์ของเคปเลอร์ หรือเรียกสั้นๆ ว่า กฎของเคปเลอร์ ซึ่งมีความสำคัญต่อพัฒนาการของวงการดาราศาสตร์อย่างยิ่งยวด

ระบบโลกเป็นศูนย์กลาง

มนุษย์พยายามจะทำความเข้าใจเรื่องจักรวาล โดยทำการศึกษาการเคลื่อนที่ของวัตถุท้องฟ้ามาแต่โบราณ ประมาณ 800 ปีก่อนคริสตกาล ชาวบาบีโลนได้สร้างปฏิทิน โดยการศึกษาการเคลื่อนที่ของดาวเคราะห์ผ่านหน้ากลุ่มดาวจักราศี 12 กลุ่ม พวกเขาได้ตั้งชื่อ ดวงอาทิตย์  ดวงจันทร์ และดาวเคราะห์ที่มองเห็นด้วยตาเปล่าทั้งห้าดวง ขึ้นเป็นชื่อวันทั้ง 7 ในสัปดาห์ คือ วันอาทิตย์ วันจันทร์ วันอังคาร วันพุธ วันพฤหัสบดี วันศุกร์ และวันเสาร์ ตามที่เราได้ใช้กันอยู่ตราบจนทุกวันนี้

เมื่อประมาณ 600 ปีก่อนคริสตกาล ไพธากอรัส (Pythagoras) นักปราชญ์ชาวกรีก ได้สร้างแบบจำลองของจักรวาลว่า โลกของเราเป็นทรงกลมตั้งอยู่ ณ ศูนย์กลาง ถูกห้อมล้อมด้วยทรงกลมขนาดใหญ่ เรียกว่า ทรงกลมท้องฟ้า (Celestial sphere) ดวงดาวทั้งหลายติดอยู่บนทรงกลมท้องฟ้านั้น ซึ่งเคลื่อนที่จากทางทิศตะวันออกไปยังทิศตะวันตก

คนในยุคก่อนสังเกตการเคลื่อนที่ของดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ทั้งห้า สวนทางกับกลุ่มดาวจักราศีทั้งสิบสอง ซึ่งตั้งอยู่บนทรงกลมท้องฟ้า จึงคิดสร้างเป็น “ปฏิทิน” (Calendar) ขึ้นมาโดยมีชื่อของดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์เป็น “ชื่อวัน” (Day) และมีชื่อของกลุ่มดาวจักราศีเป็น “ชื่อเดือน” (Month)

สมัยถัดมาราว 350 ปีก่อนคริสตกาล อริสโตเติล นักปราชญ์ชาวกรีกผู้ยิ่งใหญ่ ได้ปรับปรุงแบบจำลองระบบสุริยะของไพธากอรัส โดยเพิ่มทรงกลมใสข้างในอีก 7 ชั้น เพื่อเป็นที่ตั้งของ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ที่มองเห็นด้วยตาเปล่าอีก 5 ดวง ได้แก่ ดาวพุธ ดาวศุกร์ ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์ ทรงกลมทั้งเจ็ดเคลื่อนที่สวนทางกับทรงกลมท้องฟ้า และเคลื่อนที่จากทางทิศตะวันตก ไปยังทิศตะวันออกด้วยความเร็วที่แตกต่างกันไป

อริสโตรเติลให้ความเห็นว่า ดวงอาทิตย์ และดวงจันทร์ เป็นทรงกลมที่สมบูรณ์ (มีผิวเรียบ) ทั้งดาวฤกษ์ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ต่างเคลื่อนที่รอบโลก ซึ่งเป็นศูนย์กลางของจักรวาล การเคลื่อนที่ของวัตถุบนโลกมีสองชนิด คือ การเคลื่อนที่ในแนวราบเรียกว่า “แรง” (Force) ส่วนการเคลื่อนที่ในแนวดิ่งเป็น “การเคลื่อนที่ตามธรรมชาติ” (Natural motion) มิได้มีแรงอะไรมากระทำ ทุกสรรพสิ่งต้องเคลื่อนที่เข้าหาศูนย์กลางของโลกเนื่องจาก “โลกเป็นศูนย์กลางของจักรวาล” (Geocentric)

ในยุคกรีกโบราณ​ คนส่วนใหญ่เชื่อในระบบโลกเป็นศูนย์กลางของจักรวาล (Geocentric) ของอริสโตเติล อย่างไรก็ตาม นักปราชญ์บางคนมีความคิดเห็นตรงกันข้าม เช่น อริสตาร์คัส

ราว 300 ปีก่อนคริสตกาล ปราชญ์ชาวกรีก ชื่อ อริสตาคัส (Aristarchus) แห่งเมืองซามอส ได้คำนวณระยะทางจากโลก ถึงดวงจันทร์และดวงอาทิตย์ รวมถึงได้พยายามหาขนาดของดาวทั้งสองด้วย และได้พบว่า ดวงอาทิตย์ มีขนาดใหญ่กว่าโลกมาก อริสตาคัส จึงเสนอแบบจำลองของจักรวาลซึ่งมี “ดวงอาทิตย์เป็นศูนย์กลาง” (Heliocentric) โดยอธิบายว่า โลกหมุนรอบตัวเองวันละ 1 รอบ จากทิศตะวันตกไปยังทิศตะวันออก ทำให้เรามองเห็นท้องฟ้าเคลื่อนที่จากทิศตะวันออกไปยังทิศตะวันตก ขณะเดียวกันโลกก็โคจรไปรอบดวงอาทิตย์ ทำให้เรามองเห็นดวงอาทิตย์เคลื่อนที่ผ่านหน้ากลุ่มดาวจักราศีทั้งสิบสอง

อย่างไรก็ตาม แนวความคิดนี้ยังไม่เป็นที่ยอมรับของคนในยุคนั้น เพราะเป็นสิ่งที่ค้านสายตา และยังไม่มีใครพิสูจน์ได้ ประกอบกับโชคไม่ดีที่ห้องสมุดอเล็กซานเดรียถูกไฟไหม้ ตำราที่อริสตาร์คัสเขียนขึ้นจึงถูกทำลายจนหมดสิ้น มีแต่หลักฐานที่เกี่ยวข้องจากผู้ที่อยู่ร่วมยุคสมัยกับเขาเท่านั้นที่หลงเหลืออยู่ แนวคิดดวงอาทิตย์เป็นศูนย์กลางของอริสตาคัสจึงต้องตกไป

ทว่าแนวคิดที่ว่าโลกเป็นศูนย์กลางของจักรวาล โดยมี ดวงจันทร์ ดวงอาทิตย์ และดาวเคราะห์อีก 5 ดวงเป็นบริวารนั้น มีปัญหาใหญ่ที่ไม่สามารถอธิบายทฤษฎีให้สอดคล้องกับปรากฏการณ์ที่สังเกตเห็นจากท้องฟ้าได้ทั้งหมด นั่นคือ การเดินถอยหลังของดาวเคราะห์ เพราะถ้าโลกเป็นศูนย์กลางของดาวต่างๆ จริง ดาวทุกดวงก็ควรจะเดินเป็นเส้นตรงพุ่งไปทางทิศเดียวเท่านั้น

ปัญหานี้ได้รับการอธิบายในราวคริสต์ศตวรรษที่ 1 โดยนักคณิตศาสตร์ ภูมิศาสตร์ โหราศาสตร์ และดาราศาสตร์ชื่อก้องอย่าง ทอเลมี (Ptolemy) โดยทอเลมีได้เพิ่ม เอพิไซเคิล (Epicycle) เข้าไปในแบบจำลองของระบบโลกเป็นศูนย์กลางจักรวาล กล่าวคือ ดาวเคราะห์ที่สังเกตเห็นว่าเดินถอยหลังนั้น เป็นเพราะดาวดวงนั้นไม่ได้โคจรรอบโลกเป็นวงกลมโดยตรง แต่โคจรรอบจุดศูนย์กลางหนึ่งๆ ซึ่งจุดศูนย์กลางนั้นโคจรรอบโลกที่เป็นศูนย์กลางอีกทอดหนึ่งนั่นเอง

อย่างไรก็ตาม แม้การอธิบายโดยใช้เอพิไซเคิลของทอเลมี จะช่วยแก้ปัญหาที่ค้างคาใจนักดาราศาสตร์มาหลายร้อยปีได้ แต่การคำนวณการโคจรของดาวต่างๆ กลับมีความยุ่งยากซับซ้อนไม่น้อย เป็นเพราะทอเลมียังยึดแนวคิดที่ว่าโลกเป็นศูนย์กลางของจักรวาลอยู่นั่นเอง ซึ่งหลังจากนี้จะมีการปฏิวัติแนวคิดในวงการดาราศาสตร์อย่างพลิกหน้ามือเป็นหลังมือโดย โคเปอร์นิคัส

ระบบดวงอาทิตย์เป็นศูนย์กลาง

ในปี ค.ศ. 1514 นิโคลัส โคเปอร์นิคัส (Nicolaus Copernicus) นักคณิตศาสตร์ ดาราศาสตร์ และบาทหลวงชาวโปแลนด์ ผู้มีประสบการณ์ในการติดตามการเคลื่อนที่ของดาวเคราะห์เป็นเวลา 20 ปี มีความคิดเห็นแย้งกับระบบคิดที่ว่า โลกเป็นศูนย์กลาง

เขาให้ความเห็นว่า การอธิบายการเคลื่อนที่ถอยหลังของดาวเคราะห์ โดยใช้วงกลมเล็กในแบบจำลองของทอเลมีนั้น เลื่อนลอยไร้เหตุผล เขาได้เขียนหนังสือชื่อ De revolutionibus orbium coelestium (ปฏิวัติความเชื่อเรื่องท้องฟ้า) นำเสนอแนวความคิดที่ว่าดวงอาทิตย์เป็นศูนย์กลางจักรวาล (Heliocentric) แทน

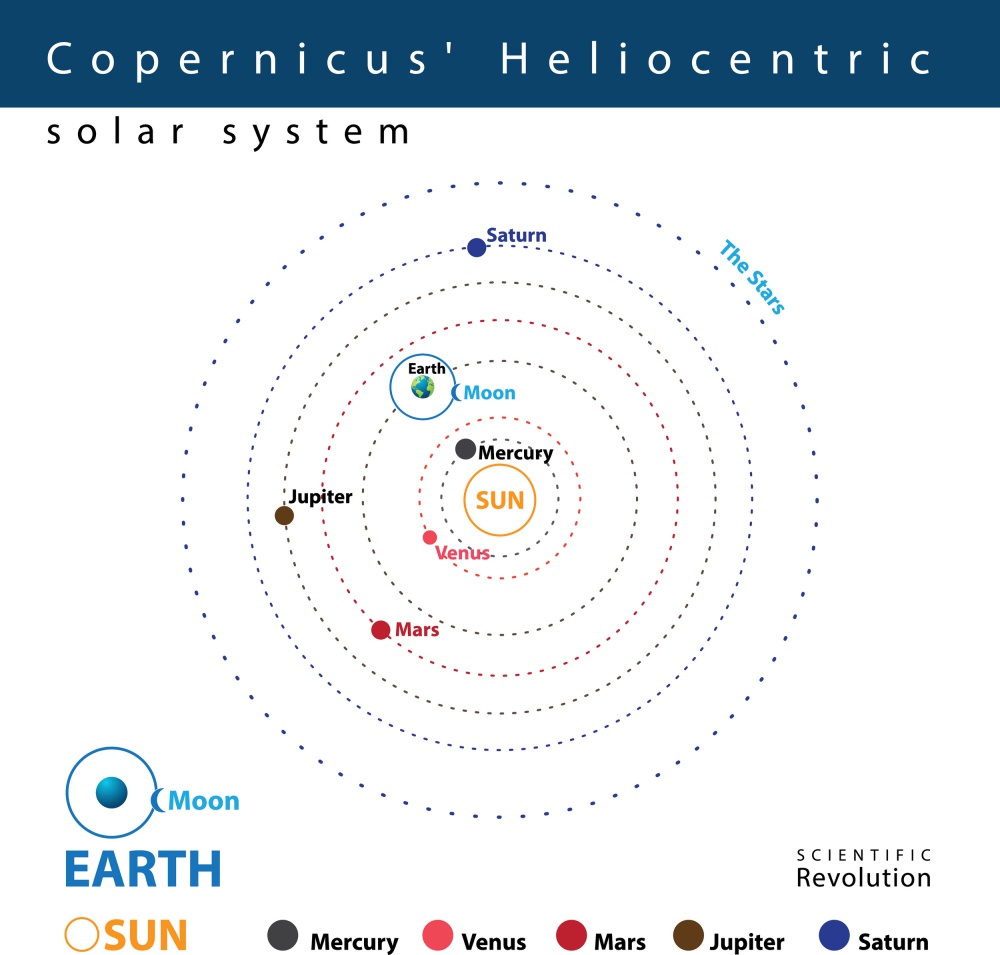
การตีพิมพ์หนังสือของโคเปอร์นิคัส ถือเป็นจุดเปลี่ยนสำคัญในประวัติศาสตร์ของวงการดาราศาสตร์ เป็นการเปลี่ยนมุมมองจากการยึดเอาโลกเป็นศูนย์กลาง มาเป็นการยึดเอาดวงอาทิตย์เป็นศูนย์กลางแทน ซึ่งทำให้การคำนวณวงโคจรของดวงดาวทำได้ง่ายกว่า และส่งผลให้ความรู้ในด้านดาราศาสตร์พัฒนาต่อไปได้อย่างกว้างขวาง

อย่างไรก็ดี การคำนวณวิถีดวงดาวจากมุมมองดวงอาทิตย์เป็นศูนย์กลางของโคเปอร์นิคัสนั้น ไม่ได้แม่นยำไปกว่าการคำนวณแบบเก่าของทอเลมี ที่มองโลกเป็นศูนย์กลาง เพียงแต่มุมมองที่ยึดดวงอาทิตย์เป็นศูนย์กลางนั้นมีความเรียบง่ายกว่ามาก ความคิดของโคเปอร์นิคัสส่งผลให้นักคิด นักวิทยาศาสตร์ต่อๆ มา นำมาต่อยอด เช่น กาลิเลโอ และเคปเลอร์

โจฮานเนส เคปเลอร์ (Johannes Kepler) นักคณิตศาสตร์ชาวเยอรมันซึ่งมีชีวิตอยู่ในระหว่าง ค.ศ. 1571-1630 ได้นำเสนอแบบจำลองสุริยจักรวาลที่มีดวงอาทิตย์เป็นศูนย์กลาง และอธิบายถึงความสัมพันธ์ของระยะห่างระหว่างดาวเคราะห์ทั้งหก (ดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์) หลังจากที่ กาลิเลโอ กาลิเลอิ (Galileo Galilei) พิสูจน์ได้ว่า ทฤษฎีดวงอาทิตย์เป็นศูนย์กลางของระบบสุริยะ (Heliocentric) นั้นถูกต้อง

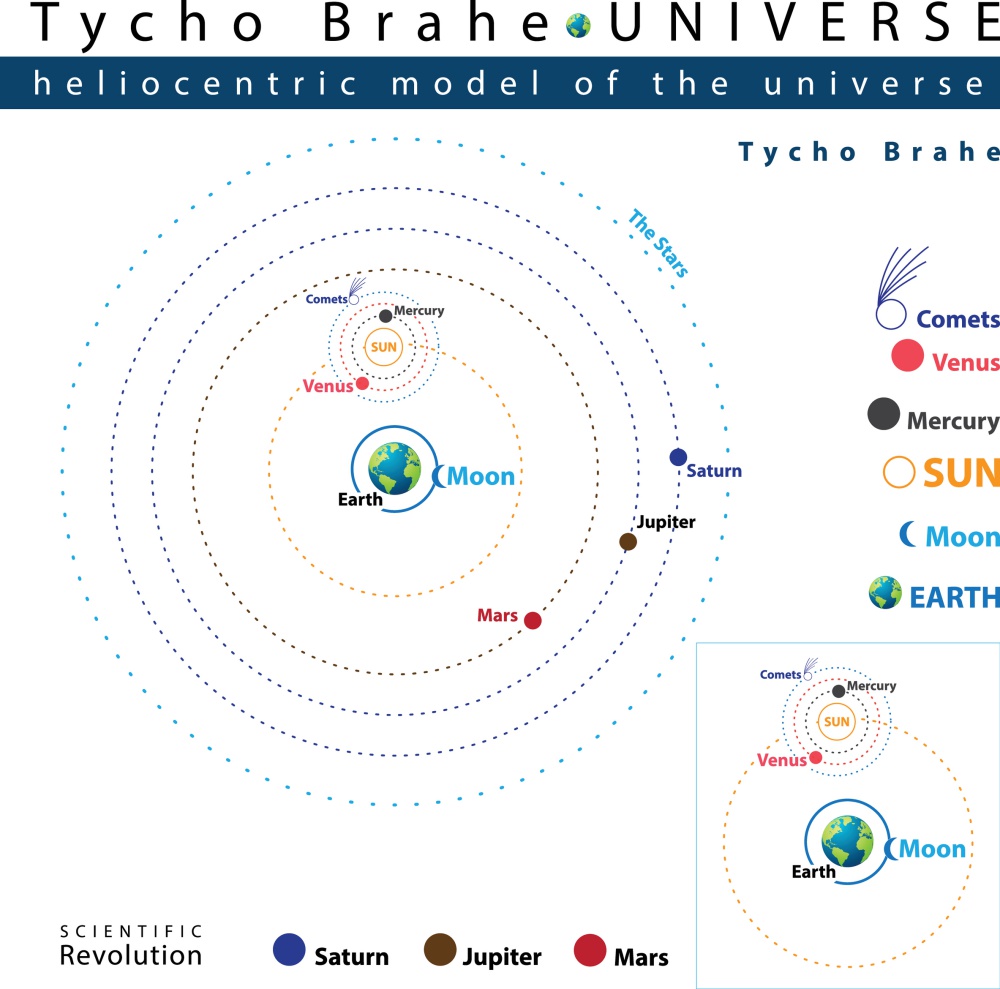
นักวิทยาศาสตร์ส่วนใหญ่คิดว่า วงโคจรของดาวเคราะห์เป็นรูปวงกลมที่สมบูรณ์ จึงไม่มีใครสามารถพยากรณ์ตำแหน่งของดาวเคราะห์ล่วงหน้าได้ถูกต้องโดยไม่ผิดเพี้ยน จนกระทั่ง เคปเลอร์ได้ทำการวิเคราะห์ข้อมูลตำแหน่งของดาวเคราะห์ ซึ่งได้มาจากการตรวจวัดอย่างละเอียดโดย ไทโค บราห์ (Tycho Brahe) นักดาราศาสตร์ประจำราชสำนักเดนมาร์ก ผู้มีชื่อเสียงในยุคนั้น (แต่ทว่าบราห์คงยังเชื่อในมุมมองโลกเป็นศูนย์กลาง) แล้วทำการทดลองด้วยแบบจำลองทางคณิตศาสตร์ จนพบในที่สุดว่า ดาวเคราะห์ในระบบสุริยะจะโคจรรอบดวงอาทิตย์เป็นรูปวงรี

ในปี ค.ศ.1609 เคปเลอร์ได้ประกาศการค้นพบกฎ 3 ข้อ ดังนี้

1. กฎแห่งวงรี: ดาวเคราะห์โคจรเป็นรูปวงรีรอบดวงอาทิตย์ โดยมีดวงอาทิตย์อยู่ที่จุดโฟกัสจุดหนึ่ง

2. กฎแห่งการกวาดพื้นที่: ในเวลาที่เท่ากัน ดาวเคราะห์จะมีพื้นที่ที่เส้นรัศมีจากดวงอาทิตย์ถึงดาวเคราะห์กวาดไปเท่ากัน

3. กฎแห่งคาบ: คาบในการโคจรรอบดวงอาทิตย์กำลังสอง แปรผันตรงกับระยะครึ่งแกนเอกของวงโคจรกำลังสาม