166,746 Views
166,746 Views
จำนวนเฉพาะ คือ จำนวนที่มีตัวประกอบเป็นจำนวนเต็มเพียงสองจำนวนเท่านั้น ที่สามารถนำมาหารจำนวนเฉพาะนี้แล้วลงตัว ซึ่งจำนวนเต็มอื่น ๆ จะไม่สามารถนำมาหารจำนวนเฉพาะได้ลงตัวเลย ยกเว้น 1 ซึ่งเป็นเอกลักษณ์ของการคูณและตัวมันเอง ยกตัวอย่างเช่น 7 เป็นจำนวนเฉพาะ เนื่องมีตัวประกอบ คือ 1 และ 7 และไม่มีจำนวนอื่น ๆ ที่นำมาหาร 7 แล้วลงตัว ในขณะที่ 6 ไม่ใช่จำนวนเฉพาะ เนื่องจาก นอกจาก 1 และ 6 แล้วยังมีจำนวนเต็มอื่น ๆ คือ 2 และ 3 ที่สามารถนำมาหาร 6 ได้ลงตัว
หลาย ๆ คนที่เริ่มพิจารณาว่าจำนวนเต็มใดเป็นจำนวนเฉพาะ มักจะเข้าใจผิดว่าจำนวนคู่ทุกจำนวนไม่เป็นจำนวนเฉพาะ เนื่องจากจำนวนคู่มีนิยามคือ จำนวนที่หารด้วย 2 แล้วลงตัวหรือมีเศษเหลือเป็นศูนย์ แต่มีข้อยกเว้นบางจำนวน นั่นคือ 2 เป็นจำนวนคู่เพียงจำนวนเดียวที่เป็นจำนวนเฉพาะ เนื่องจาก 2 มีตัวประกอบคือ 1 และ 2 เท่านั้น ไม่มีจำนวนอื่นใดที่สามารถนำมาหาร 2 แล้วลงตัว

จากความรู้เรื่องจำนวนเฉพาะนี้เราสามารถนำแนวคิดไปใช้เพื่อแก้ปัญหาเกี่ยวกับการคำนวณตัวเลขได้อย่างหลากหลาย ทั้งเรื่องการหารตัวเลข การหาตัวหารร่วมมาก หรือการหาตัวคูณร่วมน้อย การบวกลบเศษส่วน ไปจนถึงการหาเลขยกกำลัง หรือการถอดรากที่สองของจำนวน โดยเบื้องต้น เราสามารถหาจำนวนเฉพาะจาก 1 – 100 ได้จากกระบวนการที่เรียกว่า ตะแกรงเอราทอสเทนนิส ซึ่งยึดถือตามนิยามของจำนวนเฉพาะที่ว่า
กระบวนการเอราทอสเทนนิสนี้สามารถทำได้จากกระบวนการดังนี้
ขั้นตอนที่ 1 เขียนจำนวน 1 -100 โดย แบ่งเป็น 10 หลัก และ 10 แถว เรียงกัน ดังภาพ
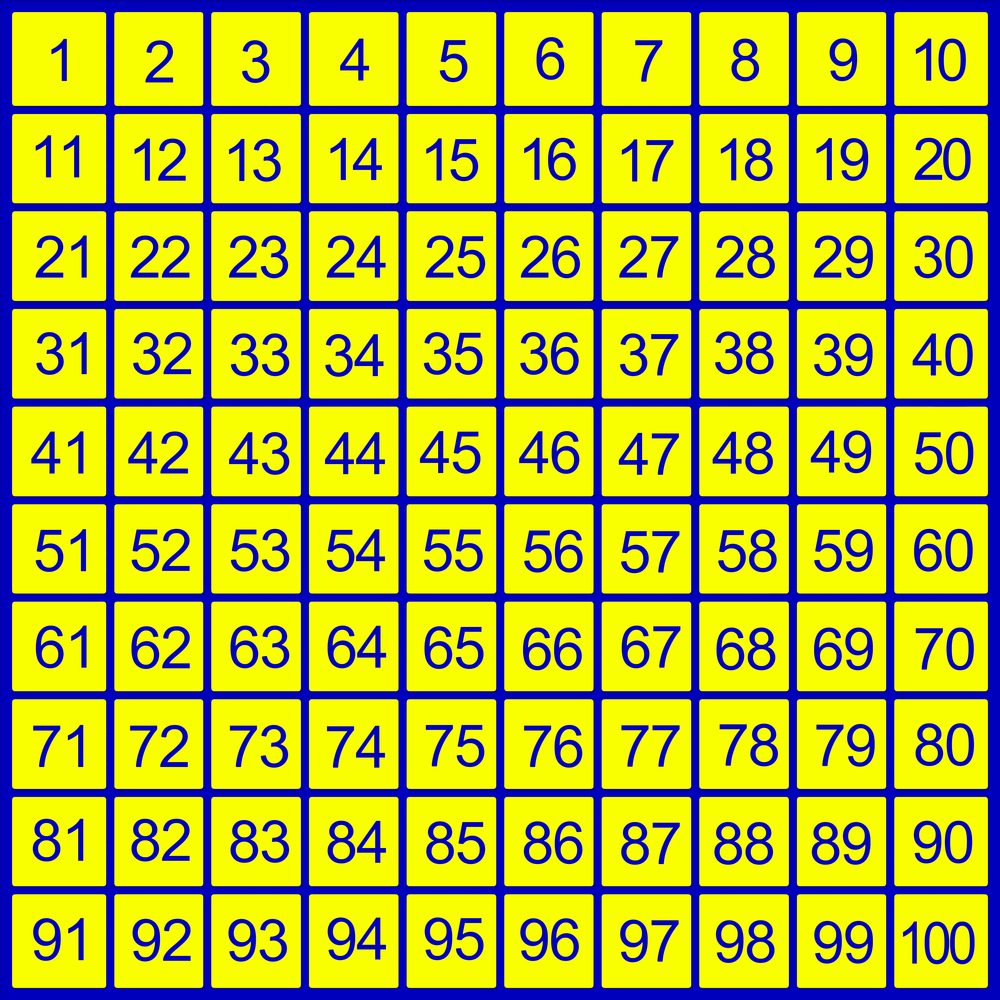
ขั้นตอนที่ 2 ตัดจำนวนคู่ทั้งหมดออก โดยยกเว้น 2 เนื่องจาก 2 เป็นจำนวนเฉพาะ

ขั้นตอนที่ 3 ตัดพหุคูณของ 5 ออก ยกเว้น 5 เนื่องจาก 5 เป็นจำนวนเฉพาะ

ขั้นตอนที่ 4 ตัดพหุคูณของ 3 ออก เช่น 9, 21, 27 เป็นต้น ยกเว้น 3 เนื่องจาก 3 เป็นจำนวนเฉพาะ

ขั้นตอนที่ 5 ตัดพหุคูณของ 7 ออก เช่น 49 เป็นต้น ยกเว้น 7 เนื่องจาก 7 เป็นจำนวนเฉพาะ

ขั้นตอนที่ 6 ตัดเลข 1 ออก เนื่องจาก 1 มีตัวประกอบ 1 ตัวคือ 1 ซึ่งไม่เป็นไปตามนิยามของจำนวนเฉพาะ