หนึ่งในสัญลักษณ์ทางคณิตศาสตร์ที่เราไม่ได้เห็นกันบ่อยนักในชีวิตประจำวัน ก็คือสัญลักษณ์ "ค่าสัมบูรณ์ (Asolute Value หรือ Modulus)" โดยมีลักษณะเป็นเส้นขีดแนวตั้งสองเส้น คร่อมจำนวนใดจำนวนหนึ่งทั้งด้านหน้าและด้านหลัง

เช่น     ค่าสัมบูรณ์ของ -5 เขียนแทนด้วยสัญลักษณ์ | -5 | ซึ่งมีค่าเท่ากับ 5
          ค่าสัมบูรณ์ของ 8 เขียนแทนด้วย | 8 | ซึ่งมีค่าเท่ากับ 8
          ค่าสัมบูรณ์ของ 4-12 เขียนแทนด้วย  | 4-12 | ซึ่งมีค่าเท่ากับ 8

หากเป็นสมการ | 8 | = 8 ดูแล้วสัญลักษณ์ค่าสัมบูรณ์จะไม่ค่อยมีความสำคัญเท่าไรนัก และเราอาจรู้สึกว่าใส่หรือไม่ใส่สัญลักษณ์ค่าสมบูรณ์คงไม่แตกต่างกัน แต่แท้จริงแล้ว ค่าสัมบูรณ์มีความหมายและสำคัญต่อการคำนวณ ทั้งยังซ่อนอยู่ในชีวิตประจำวันแบบที่เราไม่รู้ตัวเสียด้วย

ค่าสัมบูรณ์คืออะไร

ค่าสัมบูรณ์นั้นปรากฏให้เห็นครั้งแรกในข้อเขียนของ ฌอง โรเบิร์ต อาร์แกนด์ (Jean-Robert Argand) นักคณิตศาสตร์สมัครเล่นชาวสวิส เขาใช้คำว่า "absolute" และ "โมดูลัส (modulus) หรือโมดูล (module)" ในข้อเขียนดังกล่าว ซึ่งหมายถึงหน่วยวัด ในภาษาฝรั่งเศส  เพื่อระบุขนาดของเวกเตอร์และจำนวนเชิงซ้อนในการสร้างกราฟ ต่อมาในปี ค.ศ. 1841 Karl Weierstrass นักคณิตศาสตร์ชาวเยอรมันได้นำเสนอสัญลักษณ์ค่าสัมบูรณ์  | x | และนำมาใช้คำนวณทางคณิตศาสตร์กันทั่วไป

ค่าสัมบูรณ์ เป็นการบอกระยะทาง โดยไม่คำนึงถึงทิศทาง จึงมีค่าเป็นบวกหรือศูนย์เสมอ ส่วนตัวเลขหรือจำนวนในสัญลักษณ์ค่าสัมบูรณ์ จะเป็นระยะทางจากจุดศูนย์หรือจุดอ้างอิงบนเส้นจำนวนไปยังตัวเลขหรือจำนวนนั้น ๆ ตัวอย่างเช่น ค่าสัมบูรณ์ของ 8 เขียนแทนด้วย | 8 | = 8 ซึ่งหมายความว่า ระยะทางจาก 0 ถึง 8 คือ 8 หน่วย

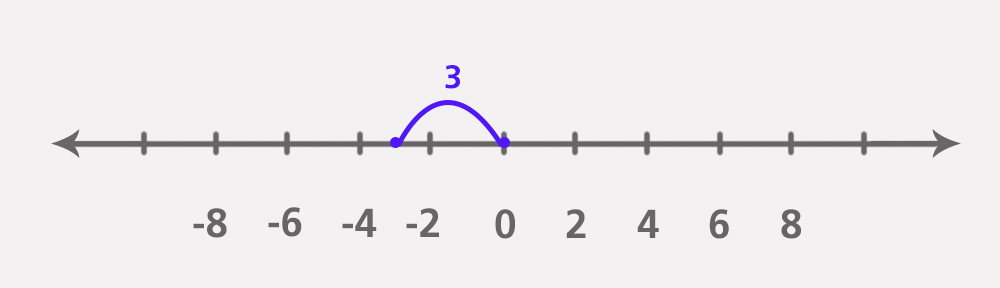
หรือ ค่าสัมบูรณ์ของ | -3 | = 3 หมายความว่า ระยะทางจาก 0 ถึง -3 คือ 3 หน่วย

ไม่เพียงบอกระยะทางเท่านั้น แต่ค่าสัมบูรณ์ยังมีความสำคัญในการสร้างกราฟค่าสัมบูรณ์อีกด้วย ตัวอย่างเช่น y = | x | - 3 จะได้คู่อันดับและสร้างกราฟได้ดังนี้

ค่าสัมบูรณ์ยังอยู่ในชีวิตประจำวันของเราโดยไม่รู้ตัว ตัวอย่างเช่น เรามีเงิน 12,000 บาท เพื่อนมีเงิน 40,000 บาท ต้องการลงทุนร่วมกันเป็นเงินคนละ 20,000 บาท
เมื่อนำเงินที่ต้องลงทุนร่วมกันหรือจุดอ้างอิงมาเป็นตัวตั้ง แล้วลบด้วยจำนวนเงินที่แต่ละคนมีอยู่ จะได้เป็น
20,000 - 12,000 = 8,000 บาท
20,000 - 40,000 = - 20,000 บาท
หากดูจากเครื่องหมายหน้าผลลัพธ์ จะกลายเป็นว่าเพื่อนมีเงินติดลบอยู่ 20,000 บาท แต่ในความเป็นจริงแล้ว เพื่อนจะเหลือเงิน 20,000 บาท หลังแบ่งไปลงทุนแล้ว ขณะที่เรายังต้องหาเงินเพิ่มอีก 8,000 บาท เพื่อมาลงทุน ดังนั้น การใส่เครื่องหมายค่าสัมบูรณ์เข้าไป จะทำให้เราทราบยอดของจำนวนเงิน โดยไม่สับสนกับทิศทาง (หรือเครื่องหมายบวกลบ) นั่นเอง

หรือในการขายสินค้า บ่อยครั้งที่เราบวกราคาสินค้าด้วยการกดเครื่องคิดเลข แล้วลบด้วยจำนวนเงินที่ลูกค้าจ่ายมา ทำให้ได้ผลลัพธ์ติดลบ ซึ่งเราจะใส่ค่าสัมบูรณ์โดยอัตโนมัติ เนื่องจากต้องการทราบเพียงจำนวนเงินที่ต้องการทอนให้ลูกค้าเท่านั้น ไม่ได้ต้องการทราบทิศทาง (กรณีนี้เราทราบทิศทางอยู่แล้ว นั่นคือ ต้องทอนเงินให้ลูกค้า)

สมการและอสมการในรูปค่าสัมบูรณ์

1. ตัวอย่างการใช้สมการในรูปค่าสัมบูรณ์ เช่น เรามีเศษเหรียญบาทอยู่ในกระเป๋า แต่ไม่แน่ใจว่ามีอยู่เท่าไร เมื่อถูกถาม จึงตอบไปว่ามีอยู่ประมาณ 20 บาท บวกลบ 5 ซึ่งกรณีนี้สามารถใช้ค่าสัมบูรณ์เพื่อหาจำนวนเหรียญบาทที่น้อยที่สุดและมากที่สุดในกระเป๋าได้ด้วยสมการ | x - 20 | = 5
กรณีที่ 1 เขียนได้เป็น x - 20  = 5 ดังนั้น x = 25
กรณีที่ 2 เขียนได้เป็น x - 20 = -5 ดังนั้น x = 15
เพราะฉะนั้นจำนวนเศษเหรียญบาทที่อยู่ในกระเป๋า จึงมีจำนวนได้ตั้งแต่ 15 ถึง 25 เหรียญ

2. ตัวอย่างการใช้อสมการในรูปค่าสัมบูรณ์ เช่น กำหนดให้โรงงานหล่อโลหะทรงกลมที่มีขนาดเส้นผ่านศูนย์กลาง 5.5 เซนติเมตร และยอมให้เกิดโอกาสคลาดเคลื่อนได้เพียง 0.05 เซนติเมตรเท่านั้น กรณีนี้สามารถใช้ค่าสัมบูรณ์เพื่อหาขนาดของเส้นผ่านศูนย์กลางทรงกลมที่โรงงานจะหล่อและลูกค้ายอมรับสินค้าได้ด้วยสมการ | x - 5.5 | ≤0.2
กรณีที่ 1 เขียนได้เป็น x - 5.5  ≤ 0.05 ดังนั้น x ≤ 5.55
กรณีที่ 2 เขียนได้เป็น - (x - 5.5) ≤ 0.05 ดังนั้น x ≥ 5.45
เพราะฉะนั้นขนาดของทรงกลมที่โรงงานจะหล่อและลูกค้ายอมรับสินค้าได้ จึงมีค่าอยู่ในช่วง 5.45 ≤ x ≤ 5.55

สมบัติของค่าสัมบูรณ์

1. | - x | = | x |
2. | xy | = | x || y |
3. l x / y l = l x l  / l y l (เมื่อ y ≠ 0)
4. | x - y | = | y - x |
5. | x | ² = x²
6. | x | =  √x²
7. | x + y | ≤ | x | +| y |
8. | x | > 0 ก็ต่อเมื่อ | x | = x
9. x < 0 ก็ต่อเมื่อ  | x | = - x
10. | x | = 0 ก็ต่อเมื่อ x = 0
11. | x - y | = 0 ก็ต่อเมื่อ x = y
12. เมื่อ x เป็นจำนวนจริงบวก
| x | ≤ y ก็ต่อเมื่อ - y ≤ x ≤ y
| x | ≥ y ก็ต่อเมื่อ x ≤ -y หรือ x ≥ y