คงเป็นเรื่องยากสักหน่อยที่จะเล่นรถไฟเหาะตีลังกาแบบไม่กรีดร้อง เพราะการเคลื่อนที่ขึ้น ๆ ลง ๆ พร้อมทั้งตีลังกากลับหัวอย่างรวดเร็วนั้น น่าจะทำให้ผู้โดยสารรู้สึกหวาดเสียวอยู่ไม่น้อย แต่เบื้องหลังของความหวาดเสียวปนความสนุกสุดเหวี่ยงนี้ มีหลักการทางวิทยาศาสตร์อย่างไรบ้าง เราจึงได้เครื่องเล่นชนิดนี้มาสร้างความบันเทิงให้กับวันที่สุดแสนจะน่าเบื่อ

รถไฟเหาะขบวนแรกของโลกเปิดตัวในปี 1884 ที่เกาะโคนีย์ (Coney Island) รัฐนิวยอร์ก ประเทศสหรัฐอเมริกา ประดิษฐ์ขึ้นโดย  LaMarcus Thompson มีความยาวประมาณ 600 ฟุต และสามารถเคลื่อนที่ได้ด้วยความเร็วสุงสุด 6 ไมล์ต่อชั่วโมง รถไฟเหาะขบวนนี้สามารถวิ่งบนรางลักษณะเป็นเนินโค้งได้ แต่มันยังไม่สามารถตีลังกาได้แบบเดียวกับรถไฟเหาะตีลังกาในปัจจุบัน รถไฟเหาะที่ขึ้นลงเนินได้นี้ใช้กฎการอนุรักษ์พลังงาน ซึ่งมีพลังงานศักย์และพลังงานจลน์เข้ามาเกี่ยวข้อง

พลังงานในการขึ้นลงเนินและตีลังกา

โดยทั่วไปแล้วรางของรถไฟเหาะจะเป็นเนินสูงต่ำ ทำให้เกิดความหวาดเสียวขณะเล่น แต่จะสังเกตว่า เนินแรกของรางมักเป็นเนินที่สูงที่สุด นั่นก็เพื่อกักเก็บพลังงานให้อยู่ในรูปของพลังงานศักย์ ก่อนจะเปลี่ยนให้กลายเป็นพลังงานจลน์ ด้วยการเคลื่อนขบวนลงมาจากจุดสูงสุด และยิ่งเนินนั้นสูงมากเท่าไร พลังงานศักย์ก็ยิ่งมีมากเท่านั้น และเปลี่ยนเป็นพลังงานจลน์ได้มากเช่นเดียวกัน พลังงานจลน์จะสูงที่สุดเมื่อขบวนรถไฟกลับลงมายังจุดต่ำสุดของรางแล้ว ดังนั้น รถไฟเหาะจึงมีแรงเคลื่อนขึ้นเนินที่เตี้ยกว่าต่อ ๆ ไปได้

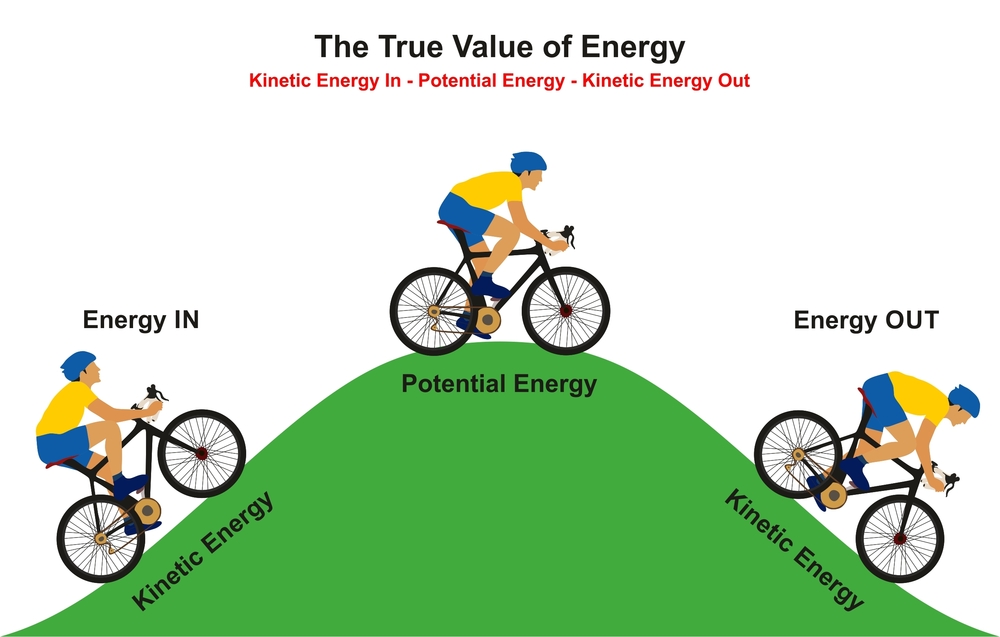
เมื่อเราพิจารณาด้วยกฎการอนุรักษ์พลังงาน ขณะที่พลังงานศักย์เปลี่ยนเป็นพลังงานจลน์ ความสูงและพลังงานศักย์จะค่อย ๆ ลดลง ส่วนพลังงานจลน์จะค่อย ๆ เพิ่มขึ้น และได้เป็น
∑ พลังงานรวมที่จุดสูงสุด = ∑ พลังงานรวมที่จุดต่ำสุด
mgh = 1/2mv²
จากสมการ ความสูงกับความเร็วจึงมีความสัมพันธ์กัน และเป็นปัจจัยหนึ่งที่จะทำให้ขบวนรถไฟขับเคลื่อนเข้าสู่วงแหวนเพื่อตีลังกาได้

การตีลังกาของรถไฟเหาะ

เครื่องเล่นที่โดดเด่นอยู่ในสวนสนุกอย่างรถไฟเหาะนี้ได้รับการพัฒนาขึ้นมาเรื่อย ๆ กระทั่งตอบสนองกลุ่มคนที่ชอบความหวาดเสียวได้มากที่สุดเมื่อมันสามารถวิ่งด้วยความเร็วสูงและตีลังกากลับหัวได้ จากหลักการทางวิทยาศาสตร์ ซึ่งประกอบด้วยแรงกระทำหลัก 2 แรง ที่ทำให้รถไฟเหาะตีลังกาหรือโรลเลอร์โคสเตอร์สามารถตีลังกาได้จริง ๆ นั่นคือ แรงแนวฉาก (Normal force) และแรงโน้มถ่วง (Force of gravity)

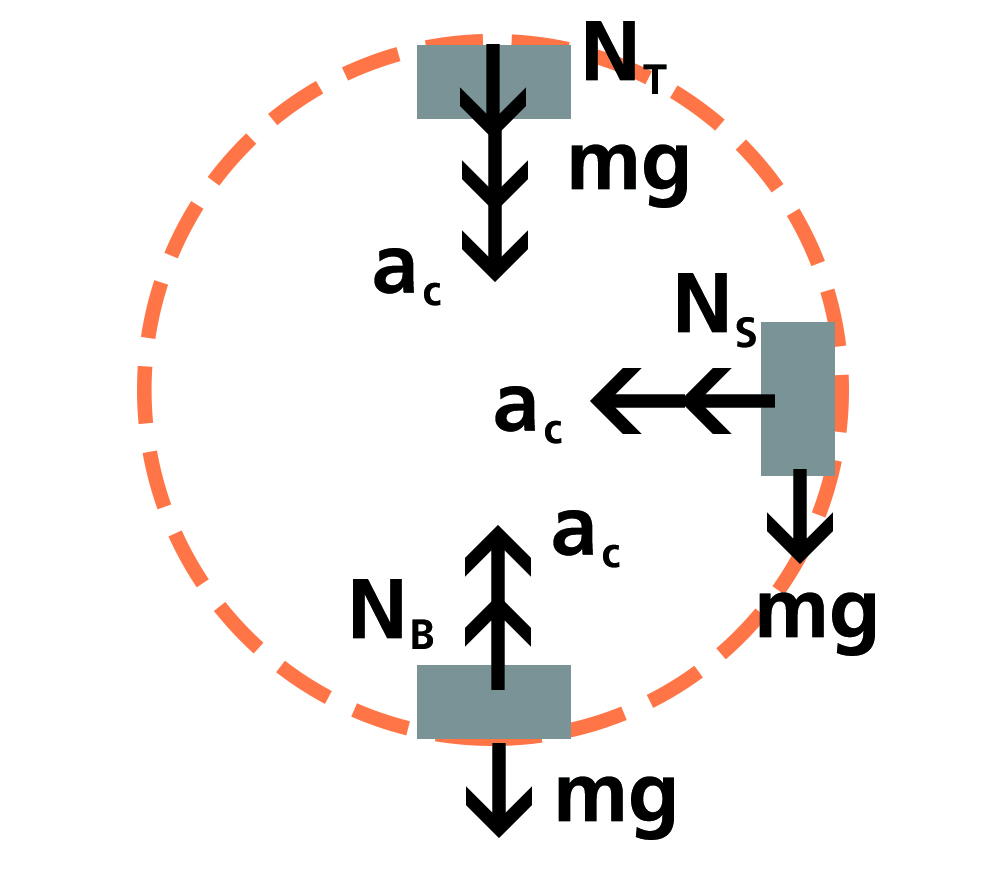
แรงแนวฉากเป็นแรงกระทำระหว่างผิววัตถุสองก้อนที่สัมผัสกัน โดยมีทิศตั้งฉากกับพื้นผิวสัมผัส ในกรณีนี้เป็นแรงที่รถไฟเหาะและรางกระทำต่อกันในแนวตั้งฉาก และเป็นเช่นนี้ไปตลอดแนวรางที่รถไฟเคลื่อนไป โดยขณะที่รถไฟเหาะวิ่งเข้าสู่รางรูปวงแหวนเพื่อตีลังกา แรงแนวฉากจะมีทิศพุ่งเข้าหาจุดศูนย์กลาง ทำให้เกิดแรงสู่ศูนย์กลาง (F_C) และมีความเร่งสู่ศูนย์กลาง (a_C) เกิดขึ้น
สูตรการหาแรงสู่ศูนย์กลาง    F_C = ma_C
สูตรการหาความเร่งสู่ศูนย์กลาง    a_C = V²/r

ส่วนแรงโน้มถ่วงเป็นแรงดึงดูดระหว่างมวลของวัตถุ ในกรณีนี้เป็นแรงที่โลกกระทำต่อรถไฟเหาะ ซึ่งจะดึงดูดโดยมีทิศเข้าสู่ศูนย์กลางโลกหรือลงด้านล่างเสมอ
สูตรการหาแรงโน้มถ่วง    F = mg    โดย g คือค่าความเร่งโน้มถ่วงของโลก มีค่าประมาณ 9.81 m/s²

จากสมการ จะสังเกตเห็นว่า ขนาดของแรงแนวฉากจะขึ้นกับความเร็วของรถไฟ รัศมีของวงแหวน และมวลของรถไฟ แต่ที่จุดสูงสุดของวงแหวน หากจะหาความเร็วที่น้อยที่สุดที่ทำให้รถไฟเหาะยังเคลื่อนไปบนรางวงแหวนได้โดยไม่หล่นลงมา จะต้องแทนค่าให้แรงแนวฉากมีค่าเป็น 0 เสมือนว่ารถไฟอยู่ในสภาพไร้น้ำหนัก จึงได้สมการเป็น    

0 =  m (V²/r) - mg

mg = m (V²/r)
V² = gr
V = √gr

ความรู้สึกสนุกที่เกิดจากแรง

แรงแนวฉากเป็นแรงที่ทำให้คนเรารู้สึกถึงน้ำหนักของตนเอง ยิ่งน้ำหนักมาก แรงแนวฉากก็ยิ่งมาก และเมื่อเราอยู่บนรถไฟเหาะที่กำลังวิ่งโดยมีความเร็วเปลี่ยนแปลงอย่างต่อเนื่อง แรงแนวฉากที่กระทำต่อเราก็เปลี่ยนแปลงไปอย่างต่อเนื่องเช่นกัน โดยขณะที่รถไฟเหาะแล่นผ่านฐานของวงแหวน ที่จุดนี้จะมีแรงกระทำต่อตัวเรามากที่สุด และเมื่อรถไฟเคลื่อนขึ้นไปถึงจุดบนสุดของวงแหวน เราจะรู้สึกถึงได้ถึงสภาวะไร้น้ำหนัก นอกจากนี้ยังมีแรงเฉื่อยที่พยายามจะรักษาตำแหน่งเดิมของร่างกายไว้ ทำให้เกิดการเหวี่ยง หรือการที่ตัวเราถูกดันไปติดกับพนักที่นั่ง ซึ่งการเปลี่ยนแปลงของแรงที่กระทำต่อตัวเราเหล่านี้ทำให้เรารู้สึกสนุก ตื่นเต้นตลอดเวลาขณะที่นั่งอยู่บนรถไฟเหาะ

ความสนุกสุด ๆ จากการเล่นรถไฟเหาะเพิ่มขึ้นไปอีกขั้นเมื่อวิศวกรได้ออกแบบรางรถไฟให้เป็นมีลักษณะม้วนเป็นหยดน้ำทรงคว่ำแทนที่จะเป็นวงกลมแบบเดิม ๆ ความสนุกเกิดขึ้นจากการที่รัศมีของวงด้านบนมีค่าน้อยกว่าด้านล่าง ทำให้ความเร่งสู่ศูนย์กลางของรถไฟที่ด้านบนมีค่ามากกว่า (จาก F_C = mV²/r) ด้านบนของวงแหวนทรงหยดน้ำจึงมีความเร็วมาก มีแรงดันให้ตัวของเราติดกับที่นั่งมากขึ้น  และเมื่อรถไฟแล่นกลับลงมา ความเร่งจะลดลง ทำให้ผู้เล่นไม่รู้สึกอึดอัดนั่นเอง

บทความที่เกี่ยวข้อง
- จักรยานกับสมดุลต่อการหมุน
- การเคลื่อนที่แนววงกลม
- การเคลื่อนที่แนววงกลมเป็นการเคลื่อนที่แบบไหน
- กฎการอนุรักษ์พลังงาน