โดยปกติแล้วเราจะหาค่าสแควรูทได้อย่างไร ถ้าไม่ใช้เครื่องคิดเลขก็ต้องคิดด้วยมือ ซึ่งบทความนี้จะเสนอวิธีประมาณค่าสแควรูทโดยการคิดด้วยมือ โดยเจ้าของวิธีคิดนี้ คือ Al – Karaji เป็นนักคณิตศาสตร์ชาวอาหรับ แต่ต้องบอกก่อนว่าวิธีการนี้เป็นวิธีตั้งแต่อดีตกาล อาจไม่ได้ให้ค่าประมาณแบบถูกต้องแม่นยำ 100% แต่ก็หาได้ใกล้เคียงมาก ๆ ซึ่งสูตรในการประมาณค่าสแควรูทของ Al – Karaji มีดังนี้

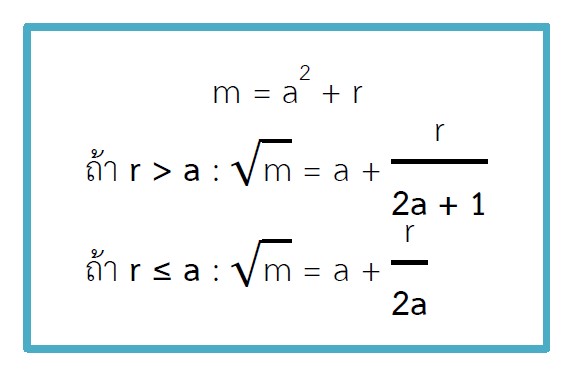
สูตรข้างต้นแตกต่างกันตรงที่ r > a มี +1 ตรงตัวส่วน แต่ r ≤ a ไม่มี +1 ตรงตัวส่วนนั่นเอง

เมื่อรู้จักสูตรและจำสูตรได้แล้ว มาดูกันว่ามันใช้อย่างไร ?

จากสูตรเราจะเห็นว่ามีทั้งหมด 3 ตัวแปร ได้แก่ m, a, r เราจะอธิบายทีละตัวแปร โดยใช้การอธิบายว่าแต่ละตัวแปรนั้นหมายถึงอะไรจากสูตร m = a² + r

               m คือ จำนวนที่เราจะหาค่าสแควรูท โดยเป็นจำนวนเต็มบวก

               a คือ จำนวนเต็มบวกที่ยกกำลัง 2 แล้วใกล้เคียง m ที่สุด (a เป็นจำนวนลบไม่ได้ เนื่องจากหากนำไปแทนค่าในสูตรแล้วจะให้คำตอบออกมาติดลบ ซึ่งจำนวนลบไม่ใช่คำตอบของสแควรูท)

               r คือ จำนวนที่บวกกับ a² แล้วเท่ากับ m (ดูจากสูตรนั่นเอง) ซึ่ง r จะเป็นจำนวนเต็มบวกหรือจำนวนเต็มลบก็ได้

               อธิบายตัวแปรแล้วอาจจะยังไม่เห็นภาพ งั้นเราลองมาดูตัวอย่างการใช้สูตรกัน !

ตัวอย่างที่ 1 :  √18 = ?   

               แอบนึกถึงสมการนี้ m = a² + r ไว้ในใจ

               วิธีการคิดเป็นลำดับดังนี้

               1. จากโจทย์เราได้ว่า m = 18 (m คือ จำนวนที่เราจะหาค่าสแควรูท) เราต้องคิดก่อนว่าจำนวนอะไรเอ่ยที่ยกกำลัง 2 แล้วใกล้เคียง 18 ได้แก่ 4² = 16 และ 5² = 25 แต่ 4² = 16 มีค่าใกล้เคียงกว่าเราจึงเลือก 4² ซึ่งจะได้ว่า a = 4

               2. จาก m = a² + r และข้อ 1. จะได้ว่า 18 = 4² + r ดังนั้น r = 2 สรุปว่า m = 18, a = 4, r = 2 นั่นเอง

               3. เลือกว่าจะใช้สูตรไหน ? จาก a = 4, r = 2 ซึ่ง a > r ดังนั้น ใช้สูตรที่ 2 นั่นคือ ถ้า r ≤ a : √m = a + (r/2a)

               4. แทนค่า m = 18, a = 4, r = 2 ลงไปในสูตรที่เราเลือก

                    √m = a + (r/2a)

                    √18 = 4 + (2/2(4))

                           = 4 + (2/8)

                           = 4 + 1/4

                           = 17/4

                           = 4.25

               ดังนั้น √18 = 4.25

จากวิธีของ Al-Karaji สามารถหาค่า √18 = 4.25 แต่ถ้าใช้วิธีการในปัจจุบันแบบตั้งหารหรือลองใช้เครื่องคิดเลข จะได้ค่า √18 ≈ 4.242... ซึ่งถือว่าได้ค่าใกล้เคียงเลยทีเดียว

ตัวอย่างที่ 1 ผ่านไป เป็นอย่างไรกันบ้างคะทุกคน ยากไหม ? ยากกว่าวิธีปัจจุบันเนอะ เพราะมีสูตรให้เราต้องเลือกใช้ มันเลยทำให้เรางง ๆ จริง ๆ อาจเป็นเพราะว่าเราไม่ชินวิธีการแบบนี้มากกว่า ฮ่า ๆ อ่ะเดี๋ยวเรามาลองตัวอย่างที่ 2 กันเลย 

ตัวอย่างที่ 2 : √35 = ?

วิธีทำ        จาก     m = a² + r

               จะได้    35 = 6² + (-1)          

(a คือ หาจำนวนที่ยกกำลัง 2 แล้วใกล้เคียง 35 ที่สุด, r คือจำนวนที่บวก a² แล้วได้ 35)             

               ดังนั้น a = 6, r = -1

               จึงเลือกใช้สูตร r ≤ a : √m = a + (r/2a)

               แทนค่า √35 = 6 + (-1/2(6))

                                = 6 - 1/12

                                = 71/12

                                = 5.91666...

               ดังนั้น  √35 ≈ 5.917

จากวิธีของ Al-Karaji สามารถหาค่า √35 ได้ประมาณ 5.917 แต่ถ้าใช้วิธีการในปัจจุบันแบบตั้งหารหรือลองใช้เครื่องคิดเลข จะได้ค่า √35 ประมาณ 5.916 ซึ่งถือว่าได้ค่าใกล้เคียงมาก ๆ เลย

เป็นอย่างไรกันบ้างคะกับการหาค่าสแควรูทจากสูตรของ Al – Karaji จริง ๆ แล้วไม่ยากเลยใช่มั้ยล่ะ ถ้าคุณผู้อ่านเข้าใจวิธีการใช้สูตรและลองฝึกบ่อย ๆ ก็จะทำได้ง่าย ๆ เลย วิธีนี้สามารถนำไปใช้ได้จริง หากเราต้องการใช้ค่าประมาณสแควรูทที่ไม่มีความละเอียดมากนัก เช่น ทศนิยม 1 ตำแหน่ง เพราะถ้าละเอียดมากกว่านี้ เช่น ทศนิยม 2 ตำแหน่งขึ้นไป อาจทำให้ค่าประมาณคลาดเคลื่อนได้ ดังนั้นการเลือกใช้วิธีหาค่าประมาณสแควรูท (ใช้สูตรของ Al – Karaji, การตั้งหาร, ใช้เครื่องคิดเลข) ให้เลือกจากความเหมาะสมที่จะใช้ค่าประมาณของเราว่าต้องการความละเอียดมากน้อยเพียงใดนั่นเอง ซึ่งทางผู้เขียนคิดว่าสูตรของ Al – Karaji ก็เป็นอีกวิธีหนึ่งที่น่าสนใจ