

 22,660 Views
22,660 Viewsเมื่อตอนที่ 1 ผู้เขียนได้นำเสนอวิธีการแก้สมการแบบอาหรับในรูปแบบสมการ x2 + Ax = B (หรือ x2 + Ax – B = 0) ไปแล้ว ฉะนั้นในตอนที่ 2 นี้ ผู้เขียนจะนำเสนออีกรูปแบบหนึ่งซึ่งมีวิธีการแก้สมการที่น่าสนใจไม่แพ้รูปแบบแรกเลย
เรามาดูวิธีการแก้สมการแบบอาหรับในรูปแบบนี้กัน!
ตัวอย่าง x2 + 21 = 10x
เริ่มต้นแก้สมการเหมือนรูปแบบที่แล้ว ทำแบบไหนนะ จำได้ไหม? นั่นคือเราต้องสร้างรูปสี่เหลี่ยมโดยให้มีพื้นที่ตามที่สมการกำหนด จาก x2 + 21 = 10x จะเริ่มสร้างรูปสี่เหลี่ยมที่มีพื้นที่เท่ากับ x2 ตารางหน่วยก่อน แล้วจึงสร้างรูปสี่เหลี่ยมที่มีพื้นที่ 21 ตารางหน่วยต่อ
1. สร้างรูปสี่เหลี่ยมที่มีพื้นที่ x2 ตารางหน่วย นั่นคือรูปสี่เหลี่ยมจัตุรัสที่มีความยาวของด้านเท่ากับ x หน่วย
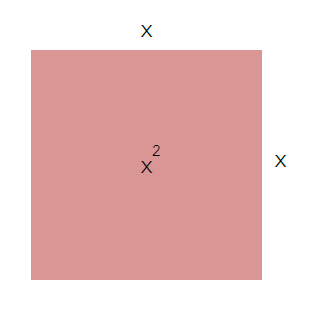
2. สร้างรูปสี่เหลี่ยม (สีฟ้า) ต่อจากรูปสี่เหลี่ยมในขั้นตอนที่ 1 (สีแดง) แล้วกำหนดว่ารูปสี่เหลี่ยมสีฟ้ามีพื้นที่เท่ากับ 21 ตารางหน่วย จากสมการ x2 + 21 = 10x เราจะได้ว่าพื้นที่ของรูปสี่เหลี่ยมสีแดงรวมกับพื้นที่ของรูปสี่เหลี่ยมสีฟ้าจะมีพื้นที่เท่ากับ 10x ตารางหน่วย ดังนั้น จะได้รูปสี่เหลี่ยมที่มีความยาวของด้านยาวเท่ากับ 10 หน่วย และความยาวของด้านกว้างเท่ากับ x หน่วย ดังรูป
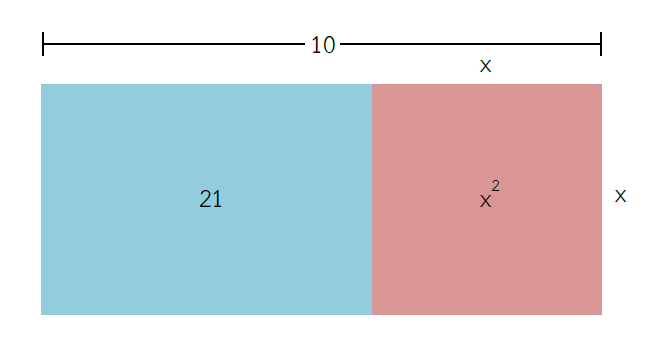
3. แบ่งครึ่งด้านยาวจะได้ความยาวครึ่งละ 5 หน่วย จากนั้นลากเส้นแบ่งครึ่งรูปสี่เหลี่ยม (จากขั้นตอนที่ 2) ทำให้เกิดรูปสี่เหลี่ยมสีม่วงขึ้น (จริง ๆ เดิมก็คือสีฟ้านั่นแหละ แต่เปลี่ยนเป็นสีม่วงเพื่อให้เห็นชัดเจนขึ้น พื้นที่สีฟ้ารวมกับสีม่วงเท่ากับ 21 ตารางหน่วยเหมือนเดิมจ้า) โดยรูปสี่เหลี่ยมสีม่วงจะมีความยาวของด้านยาวเท่ากับ x หน่วย และความยาวของด้านกว้างเท่ากับ 5 – x หน่วย ดังรูป
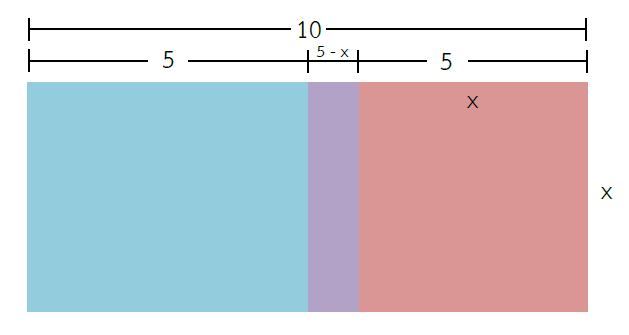
4. ต่อเติมรูปโดยนำรูปสี่เหลี่ยมสีม่วงไปแปะใต้รูปสี่เหลี่ยมสีฟ้า ดังรูป พิจารณารูปสี่เหลี่ยมสีฟ้าที่มีความยาวด้านกว้างเท่ากับ x หน่วยต่อกับรูปสี่เหลี่ยมสีม่วงที่มีความยาวด้านกว้างเท่ากับ 5 – x หน่วย ดังนั้น จะมีความยาวด้านรวมเป็น 5 หน่วย ดังรูป
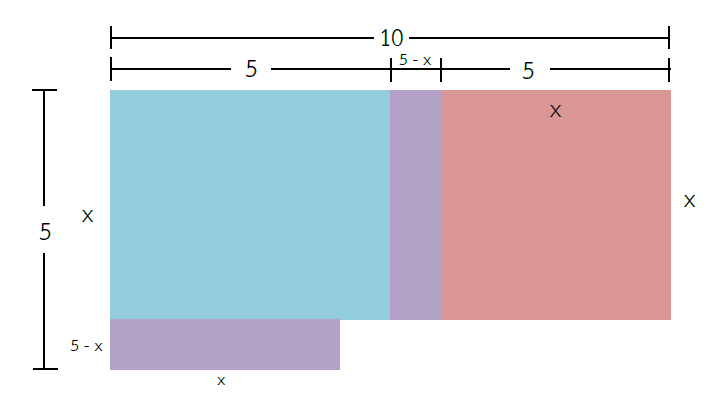
5. สร้างรูปสี่เหลี่ยมสีเขียว ซึ่งจะมีความยาวของด้านแต่ละด้านเท่ากับ 5 – x หน่วย ดังรูป
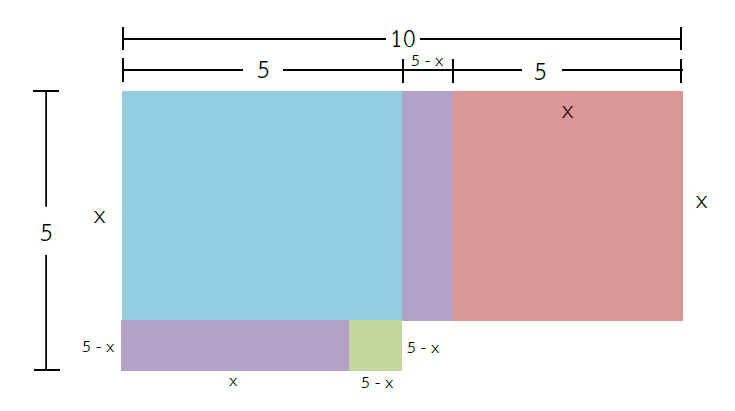
6. จากรูปในขั้นตอนที่ 5 เราจะหาพื้นที่รูปสี่เหลี่ยมสีเขียวได้อย่างไรกันนะ อ่ะมาดูกัน
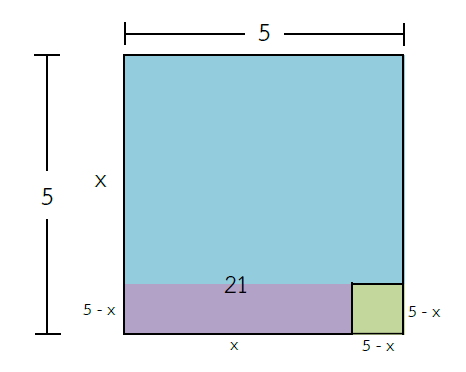
พิจารณารูปสี่เหลี่ยมใหญ่ที่ประกอบด้วยรูปสี่เหลี่ยมสีฟ้า รูปสี่เหลี่ยมสีม่วง และรูปสี่เหลี่ยมสีเขียว จากรูปเรารู้ข้อมูลอะไรบ้าง ? รูปสี่เหลี่ยมใหญ่นี้จะมีความยาวแต่ละด้านเท่ากับ 5 หน่วย (เป็นรูปสี่เหลี่ยมจัตุรัสนั่นเอง) และพื้นที่สีฟ้ากับสีม่วงรวมกันมีพื้นที่เท่ากับ 21 ตารางหน่วย ดังนั้น เราจะหาพื้นที่สีเขียวได้จากพื้นที่รูปสี่เหลี่ยมจัตุรัสรูปใหญ่ลบออกด้วยพื้นที่สีฟ้าและสีม่วง
เขียนเป็นสมการได้ดังนี้
พื้นที่ของรูปสี่เหลี่ยมสีเขียว = พื้นที่รูปสี่เหลี่ยมจัตุรัสรูปใหญ่ - (พื้นที่สีฟ้า + พื้นที่สีม่วง)
= (5 x 5) – 21
= 25 - 21
= 4 ตารางหน่วย
7. เรารู้ข้อมูลอะไรเกี่ยวกับรูปสี่เหลี่ยมสีเขียวบ้าง ? เรารู้ว่ารูปสี่เหลี่ยมสีเขียวเป็นรูปสี่เหลี่ยมจัตุรัส มีความยาวด้านแต่ละด้านเท่ากับ 5 – x หน่วย (จากขั้นตอนที่ 5) พื้นที่รูปสี่เหลี่ยมสีเขียวเท่ากับ 4 ตารางหน่วย (จากขั้นตอนที่ 6) สามารถเขียนเป็นสมการและแก้สมการหาค่าของตัวแปรได้ดังนี้
พื้นที่รูปสี่เหลี่ยมสีเขียว = 4 ตารางหน่วย
(5 - x)(5 – x) = 4
(5 – x)2 = 4
(5 – x)2 = 22
5 – x = 2
x = 3
จากสมการ x2 + 21 = 10x เราได้คำตอบ x = 3 นั่นเอง
เมื่อทำความเข้าใจการแก้สมการทั้ง 2 รูปแบบของอัลควาริซมีแล้วนั้น อาจเกิดความคิดว่า อัลควาริซมีไม่น่าจะคิดวิธีการแก้โจทย์แบบนี้ขึ้นมาเลย มันค่อนข้างซับซ้อน ค่อนข้างใช้เวลาทำความเข้าใจ ถ้าเป็นปัจจุบันใช้วิธีการแยกตัวประกอบคงง่ายกว่า ไม่ยุ่งยากซับซ้อนเท่าวิธีของอัลควาริซมี แต่เราก็ต้องคิดว่าสมัยนั้นยังไม่มีการแยกตัวประกอบเกิดขึ้น ดังนั้น จึงต้องใช้วิธีแบบนี้ในการแก้สมการ และอัลควาริซมีเหตุผลในการคิดเรื่องนี้ขึ้น เพื่อเป็นประโยชน์ในเรื่องการค้า การแบ่งสมบัติ การวัดที่ดิน และอื่น ๆ อีกมากมาย
บทความที่เกี่ยวข้อง
- แก้สมการแบบอาหรับ (ตอนที่ 1)
