
 22,148 Views
22,148 Viewsเขาคนนั้นคือ อัลควาริซมี Al-Khwarizmi (ค.ศ. 780 - 850) เป็นนักคณิตศาสตร์แห่งอาหรับที่คิดค้นวิชาพีชคณิตของโลก (วิชาคณิตศาสตร์ที่ว่าด้วยการแก้สมการ) เขาได้ชื่อว่าเป็นบิดาแห่งพีชคณิต และแต่งตำราอัลญับรุ้ วัล มุกอบะละฮฺ ซึ่งเป็นตำรามาตรฐานในการศึกษาวิชาพีชคณิตอันเป็นตำราที่อัลควาริซมีได้แต่งขึ้นเป็นคนแรก และชาวตะวันตกก็ได้รู้จักวิชาพีชคณิตจากตำราเล่มนี้ แล้วเรียกวิชาพีชคณิตว่า Algebra ซึ่งมาจากคำว่า อัลญับรุ้ (الجبر)
.jpg)
ทั้งนี้อัลควาริซมียังได้ปรับปรุงและพัฒนาความคิดในเชิงคณิตศาสตร์ด้วยการคิดระบบแบบใหม่ในการแก้สมการ โดยเฉพาะสมการในพีชคณิตที่มีกำลังสองตามหลักพีชคณิตและเรขาคณิตอีกด้วย
เหนือสิ่งอื่นใด อยากให้คุณผู้อ่านนั้นลืมการแก้สมการแบบแยกตัวประกอบไปเสียก่อน เสมือนว่าเราไม่เคยเรียนรู้วิธีการแก้สมการมาก่อน โดยการแก้สมการแบบอาหรับนั้นจะใช้ความรู้ตามหลักพีชคณิตและเรขาคณิต กล่าวคือเราจะใช้เรื่องพื้นที่ของรูปสี่เหลี่ยม (กว้าง x ยาว) เข้ามาช่วยในการแก้สมการ โดยเราต้องสร้างพื้นที่รูปสี่เหลี่ยมแบบต่าง ๆ จากสมการ แล้วสังเกตรูปที่สร้างเพื่อหาค่าของตัวแปร จะเป็นอย่างไรเดี๋ยวมาดูกัน
บทความนี้จะนำเสนอรูปแบบสมการทั้งหมด 2 รูปแบบ ได้แก่ x2 + Ax = B (หรือ x2 + Ax – B = 0) และ x2 + Q = Px (หรือ x2 – Px + Q = 0)
เรามาดูวิธีการแก้สมการแบบอาหรับในรูปแบบนี้กัน!
ตัวอย่าง x2 + 20x = 125
จากสมการ x2 + 20x = 125 เราจะสร้างพื้นที่ x2 + 20x หน่วย แล้วกำหนดว่าพื้นที่ดังกล่าวเท่ากับ 125 ตารางหน่วย เรามาสร้างพื้นที่ทีละพจน์กัน
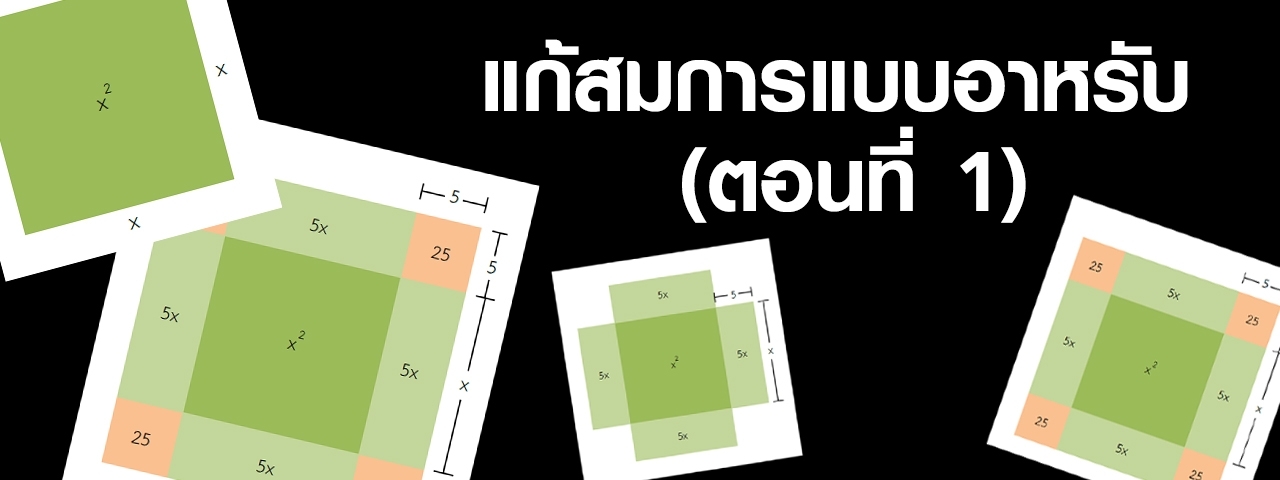
1. สร้างรูปสี่เหลี่ยมที่มีพื้นที่เท่ากับ x2 คุณผู้อ่านคิดว่าสามารถสร้างรูปสี่เหลี่ยมได้ในลักษณะใด ติ๊กต่อก ๆ ๆ แอ๊ดดดด หมดเวลา รูปสี่เหลี่ยมนั้นคือรูปสี่เหลี่ยมจัตุรัสที่มีความยาวด้านเท่ากับ x หน่วยนั่นเอง ดังรูป
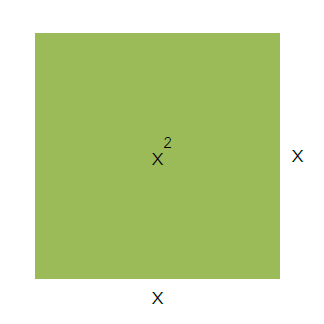
2. สร้างรูปสี่เหลี่ยมที่มีพื้นที่เท่ากับ 20x ตารางหน่วยต่อเพิ่มจากขั้นตอนแรก ดังนั้นเราจะสร้างรูปสี่เหลี่ยมที่มีพื้นที่เท่ากับ 5x ตารางหน่วย นำมาต่อด้านทั้งสี่ด้านของรูปสี่เหลี่ยมจัตุรัส เมื่อรวมทั้ง 4 รูปจะมีพื้นที่เท่ากับ 20x ตารางหน่วยนั่นเองจ้า ดังรูป
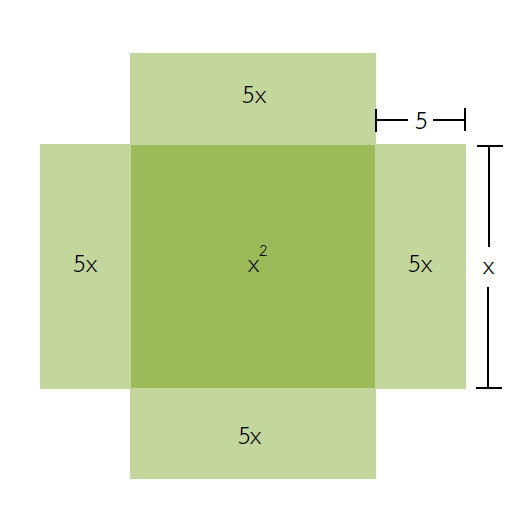
3. สร้างรูปสี่เหลี่ยมสีส้ม ซึ่งจะมีด้านแต่ละด้านเท่ากับ 5 หน่วย ดังนั้นมีพื้นที่แต่ละรูปเท่ากับ 25 ตารางหน่วย ดังรูป
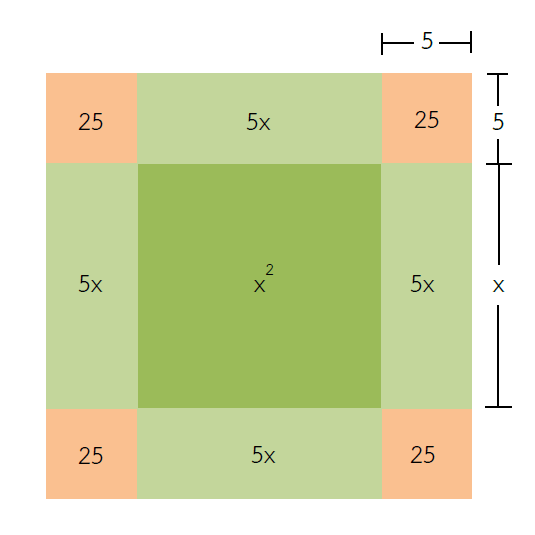
4. สังเกตรูปแล้วสร้างสมการเพื่อหาค่าของตัวแปร ให้มองรูปสี่เหลี่ยมจัตุรัสใหญ่ที่ประกอบด้วยรูปสี่เหลี่ยมสีเขียวจำนวน 5 รูปและรูปสี่เหลี่ยมสีส้มจำนวน 4 รูป ซึ่งจะมีความยาวของด้านเท่ากับ x + 10 หน่วย ดังรูป จะได้ว่าพื้นที่ของรูปสี่เหลี่ยมจัตุรัสใหญ่เท่ากับพื้นที่ของรูปสี่เหลี่ยมสีเขียวรวมกับพื้นที่ของรูปสี่เหลี่ยมสีส้ม
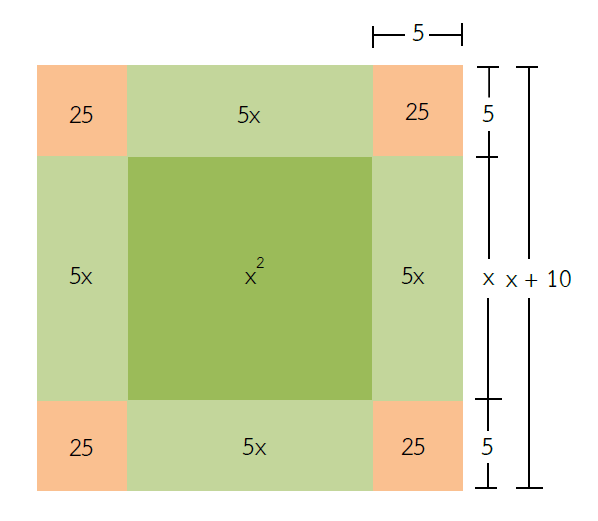
เมื่อนำมาเขียนเป็นสมการ จะได้
พื้นที่ของรูปสี่เหลี่ยมจัตุรัสใหญ่ = พื้นที่ของรูปสี่เหลี่ยมสีเขียว + พื้นที่ของรูปสี่เหลี่ยมสีส้ม
(x + 10)2 = 125 + 25(4)
= 125 + 100
= 225
(x + 10)2 = 152
x + 10 = 15
x = 5
จากสมการ x2 + 20x = 125 เราได้คำตอบ x = 5 นั่นเอง
นี่เป็นขั้นตอนการแก้สมการแบบอาหรับในรูปแบบแรก x2 + Ax = B (หรือ x2 + Ax – B = 0) คุณผู้อ่านคิดว่ายากไหม ? อย่าเพิ่งท้อแท้นะ ฮ่า ๆ ส่วนตัวผู้เขียนคิดว่าการแก้สมการแบบนี้เป็นวิธีการที่น่าสนใจ ฝึกให้คิดเชื่อมโยง ทำให้เกิดทักษะทางคณิตศาสตร์เพิ่มขึ้นด้วย ยังมีอีกรูปแบบที่เราจะไปเรียนรู้กัน ติดตามต่อได้ในหัวข้อแก้สมการแบบอาหรับ (ตอนที่ 2) จ้า!
บทความที่เกี่ยวข้อง
- แก้สมการแบบอาหรับ (ตอนที่ 2)
