

 91,832 Views
91,832 Views
นั่นคือ พื้นที่ของรูปสี่เหลี่ยม = ความยาวของด้านกว้าง x ความยาวของด้านยาว หรือที่ท่องจำกันว่า กว้าง x ยาว
โดยในที่นี้จะนำมาใช้อธิบายสูตรกำลังสองสมบูรณ์ (บวก)
หน้าตาของสูตรกำลังสองสมบูรณ์ (บวก) เป็นดังนี้
(a + b)2 = a2 + 2ab + b2
จากสมการดังกล่าว เราสามารถเปลี่ยนเป็นภาพได้ ดังนี้
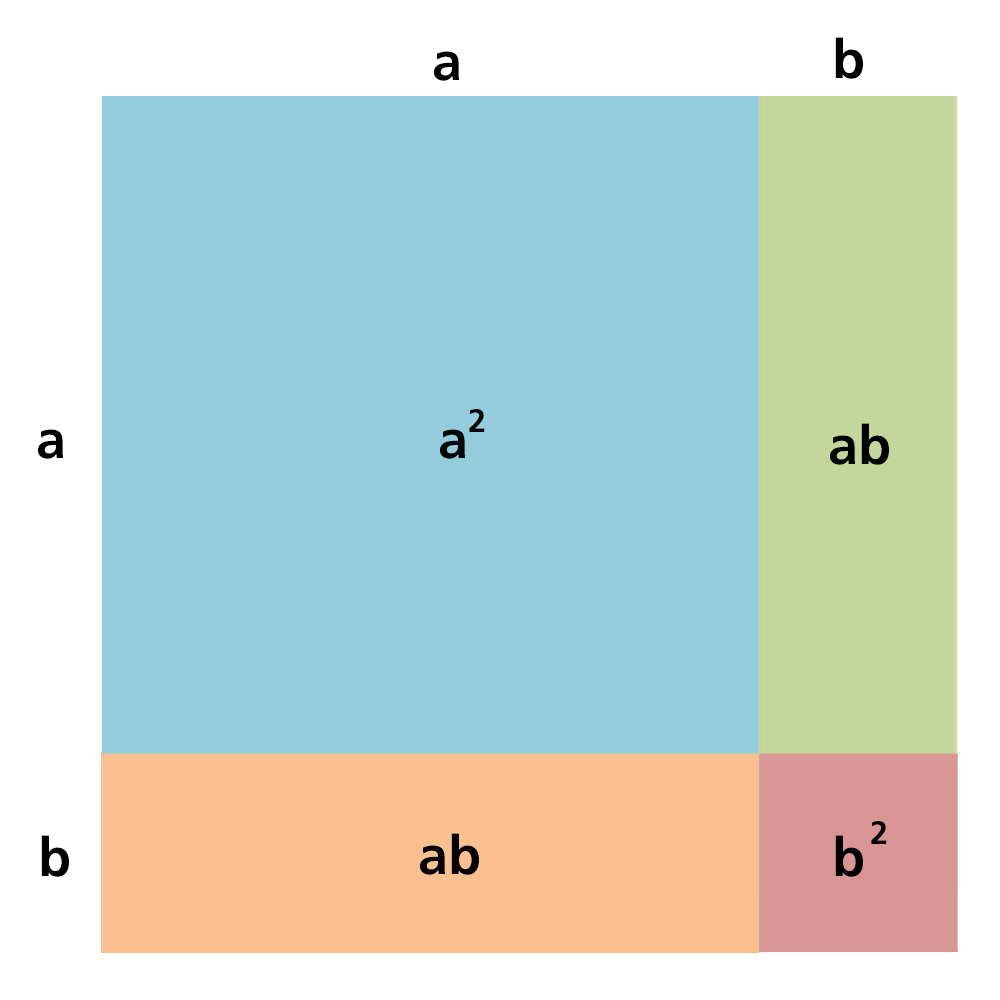
จากภาพให้สังเกตที่รูปสี่เหลี่ยมใหญ่ที่สุดก่อน นั่นคือ รูปสี่เหลี่ยมที่มีความยาวด้านเท่ากับ a + b หน่วย
จะได้พื้นที่ของรูปสี่เหลี่ยมนี้ = (a + b)(a + b) = (a + b)2 ตารางหน่วย
ต่อไปให้พิจารณารูปสี่เหลี่ยมเล็กแต่ละรูปที่ประกอบขึ้นเป็นรูปสี่เหลี่ยมใหญ่ ซึ่งมีทั้งหมด 4 รูป ได้แก่ รูปสี่เหลี่ยมสีฟ้า รูปสี่เหลี่ยมสีแดง รูปสี่เหลี่ยมสีเขียว และรูปสี่เหลี่ยมสีส้ม
รูปสี่เหลี่ยมสีฟ้า มีความยาวด้านแต่ละด้านเท่ากับ a หน่วย ดังนั้น พื้นที่ของรูปสี่เหลี่ยมสีฟ้า = a x a = a2 ตารางหน่วย
รูปสี่เหลี่ยมสีแดง มีความยาวด้านแต่ละด้านเท่ากับ b หน่วย ดังนั้น พื้นที่ของรูปสี่เหลี่ยมสีแดง = b x b = b2 ตารางหน่วย
รูปสี่เหลี่ยมสีเขียว มีความยาวด้านยาวเท่ากับ a หน่วย และมีความยาวด้านกว้างเท่ากับ b หน่วย ดังนั้น พื้นที่ของรูปสี่เหลี่ยมสีเขียว = a x b = ab ตารางหน่วย
รูปสี่เหลี่ยมสีส้ม มีความยาวด้านยาวเท่ากับ a หน่วย และมีความยาวด้านกว้างเท่ากับ b หน่วย ดังนั้น พื้นที่ของรูปสี่เหลี่ยมสีส้ม = a x b = ab ตารางหน่วย
จากภาพข้างต้น รูปสี่เหลี่ยมทั้ง 4 รูปที่ประกอบขึ้นเป็นรูปสี่เหลี่ยมใหญ่ ทำให้ได้ว่าพื้นที่ของรูปสี่เหลี่ยมทั้ง 4 รูปรวมกันจะเท่ากับพื้นที่ของรูปสี่เหลี่ยมใหญ่ ดังนี้
พื้นที่ของรูปสี่เหลี่ยมใหญ่ = พื้นที่รูปสี่เหลี่ยมสีฟ้า + พื้นที่รูปสี่เหลี่ยมสีแดง + พื้นที่รูปสี่เหลี่ยมสีเขียว + พื้นที่รูปสี่เหลี่ยมสีส้ม
(a + b)2 = a2 + b2 + ab + ab
(a + b)2 = a2 + 2ab + b2
จึงสรุปได้ว่า (a + b)2 = a2 + 2ab + b2 ซึ่งเป็นไปตามสูตรกำลังสองสมบูรณ์ (บวก)
