274,527 Views
Favorite
สำหรับนิยามของสแควรูทกคือ √a2 = /a/ ดังนั้น ค่าที่ได้ก็จะเป็นจำนวนบวกเสมอ
เช่น √25 = √52 = /5/ = 5
√(-3)2 = /-3/ = 3
เราทราบที่มาของคำว่า "สแควรูท" ได้จากการสร้างกราฟขึ้นมา ซึ่งในที่นี้จะยกตัวอย่าง 42 หรือ 4x4 เท่ากับ 16 หรือ √16 เท่ากับ 4 โดยการวาง 4 ตัวหน้าไว้บนกราฟแกนนอน (x) และวาง 4 ตัวหลังไว้บนกราฟแกนตั้ง (y) ก็จะได้รูปสี่เหลี่ยมจัตุรัส (Square) ที่มีพื้นที่เท่ากับ ด้านxด้าน คือ 16 ตารางหน่วย ในทำนองเดียวกัน หากแต่ละด้านของกราฟคือ 8 หน่วย ก็จะได้สี่เหลี่ยมจตุรัสที่มีพื้นที่ 64 ตารางหน่วย จึงเป็นที่มาของคำว่า สแควรูท (Square Root) นั่นเอง
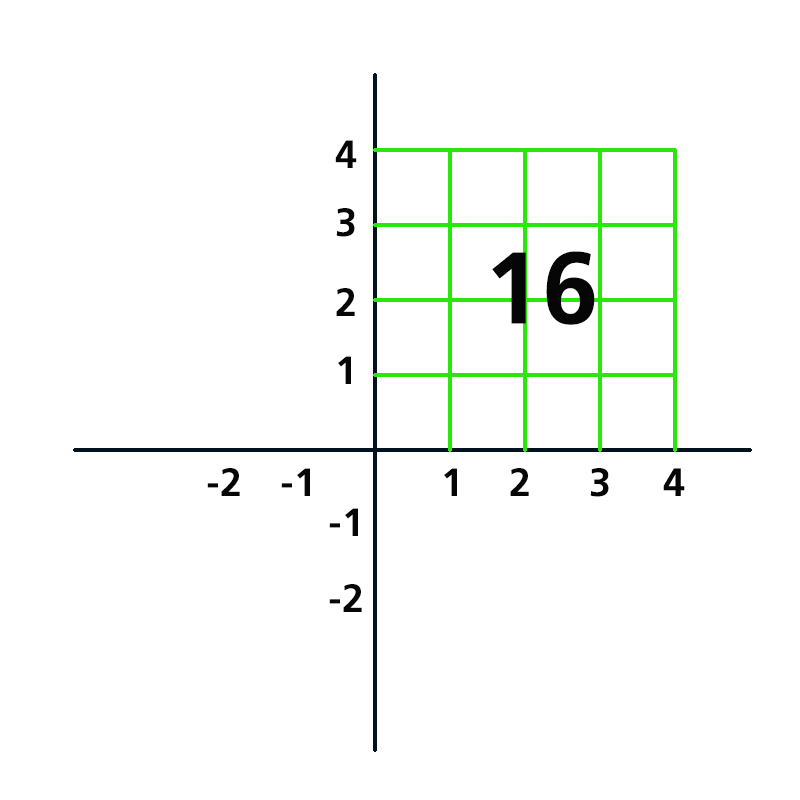
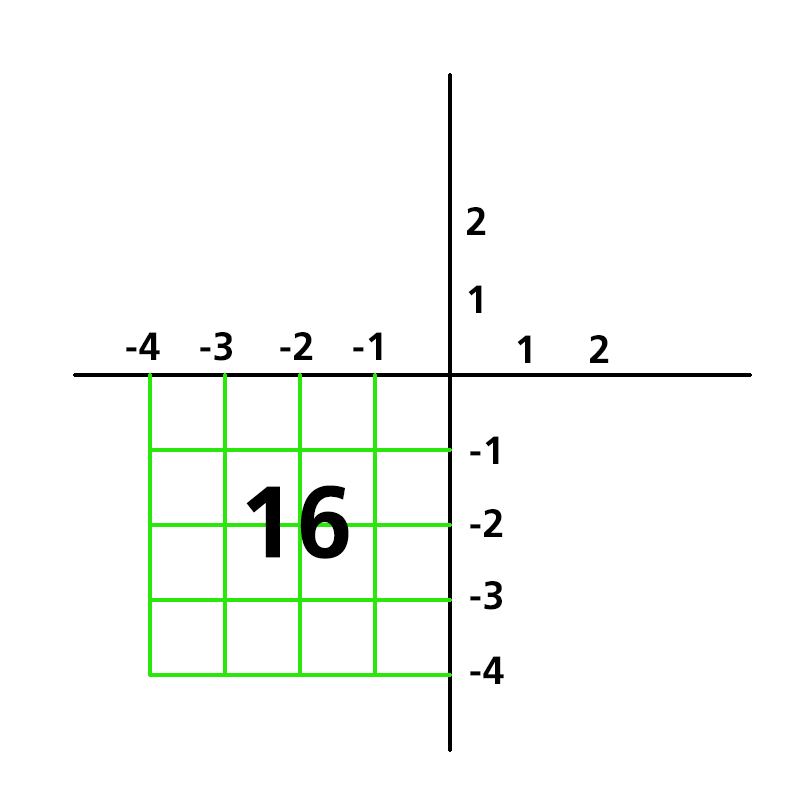
หากตัวเลขที่อยู่ในเครื่องหมายสแควรูทเป็นตัวเลขกำลังสองสมบูรณ์ (Perfect Square) เช่น 9 16 25 การถอดสแควรูทคงทำได้ไม่ยากนัก เพราะเราคุ้นเคยกันดีอยู่แล้ว
| เลขกำลังสองสมบูรณ์ | ถอดสแควรูท |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
| 169 | 13 |
| 196 | 14 |
| 225 | 15 |
| 256 | 16 |
| 289 | 17 |
| 324 | 18 |
| 361 | 19 |
| 400 | 20 |
| 441 | 21 |
| 484 | 22 |
| 529 | 23 |
| 576 | 24 |
| 625 | 25 |
ส่วนคำว่า รากที่สอง มีนิยามที่แตกต่างไปจากสแควรูทเล็กน้อย โดย ถ้า a เป็นจำนวนจริงใด ๆ แล้ว a เป็นรากที่สองของ x ก็ต่อเมื่อ a2 = x
เช่น รากที่สองของ 25 = ± 5 เพราะ 52 = 25 และ (-5)2 = 25
รากที่สองของ 121 = ±11 เพราะ 112 = 121 และ (-11)2 = 121
ดังนั้น คำตอบจากการถอดสแควรูท กับการหารากที่สองของจำนวนใดจำนวนหนึ่ง จึงได้ผลลัพธ์ที่แตกต่างกัน
ข้อสังเกตที่น่าสนใจอีกอย่างคือ เราจะไม่ได้เห็นตัวเลขในเครื่องหมายสแควรูทติดลบเลยและเราก็จะไม่เห็นรากที่สองของจำนวนจริงที่ติดลบด้วย เพราะมันไม่มีจำนวนจริงใดที่คูณด้วยตัวมันเองแล้วทำให้ผลลัพธ์ที่ได้มีค่าเป็นลบนั่นเอง
