761,999 Views
761,999 Views
แม้ว่าเราจะไม่ได้มีโอกาสประยุกต์ใช้ตรีโกณมิติในชีวิตประจำวันมากนัก (นอกจากผู้ที่เรียนสาขาวิชาคณิตศาสตร์โดยตรง นักคณิตศาสตร์ หรือวิศวกร) แต่ในบางครั้งเราก็ได้ใช้ประโยชน์จากมัน เช่น การคำนวณหาระยะทางการเดินเรือในทะเล อีกทั้งยังมีความเกี่ยวข้องสัมพันธ์กับคณิตศาสตร์ในสาขาอื่น ๆ อย่างลอการิทึม แคลคูลัส เป็นต้น
อย่างไรก็ตาม ปัญหาหนึ่งในการคำนวณเรื่องตรีโกณมิติ ก็คือ การจดจำค่าของฟังก์ชันตรีโกณมิติ โดยมีฟังก์ชันพื้นฐานอยู่ 3 ฟังก์ชัน ซึ่งเป็นค่าของแต่ละด้านที่หารด้วยอีกด้านหนึ่ง ได้แก่
***sine***
sin θ = ด้านตรงข้ามมุม θ/ด้านตรงข้ามมุมฉาก
= ข้าม/ฉาก
***cosine***
cos θ = ด้านประชิดมุม θ/ด้านตรงข้ามมุมฉาก
= ชิด/ฉาก
***tangent***
tan θ = ด้านตรงข้ามมุม θ/ด้านประชิดมุม θ
= ข้าม/ชิด
1. วาดรูปสามเหลี่ยมด้านเท่า ที่มีด้านยาวด้านละ 1 หน่วย มุมแต่ละมุมภายในรูปสามเหลี่ยมจะเท่ากับ 60ํ
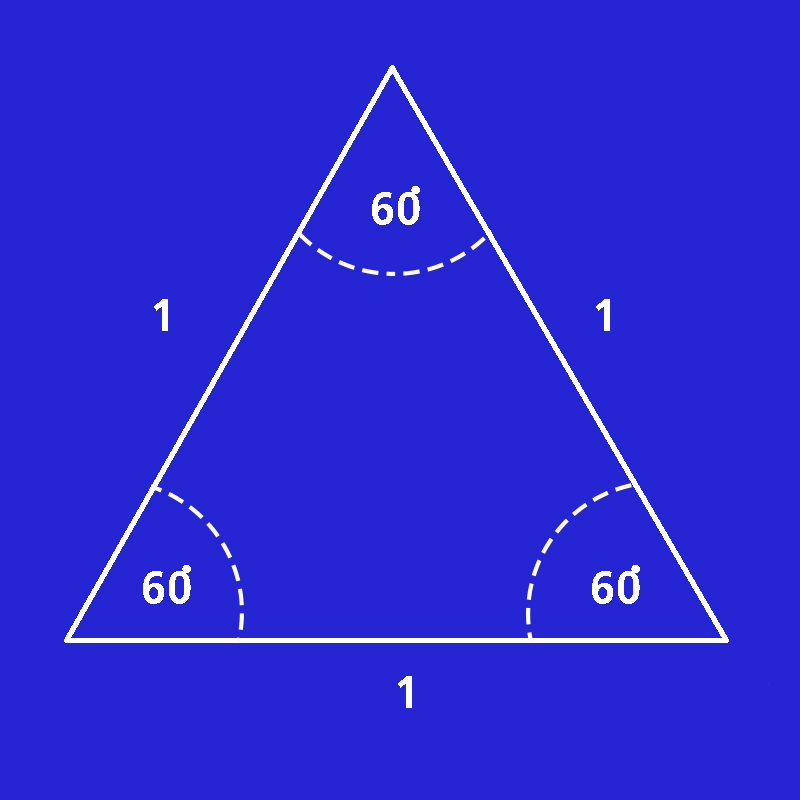
2. ลากเส้นจากมุมยอดของสามเหลี่ยมมาตั้งฉากกับฐาน เส้นนี้จะแบ่งสามเหลี่ยมด้านเท่าออกเป็น 2 รูป
3. สังเกตสามเหลี่ยมที่ถูกแบ่งแล้วรูปใดรูปหนึ่ง จะมีฐานเท่ากับ 1/2 หน่วย และด้านตรงข้ามมุมฉากเท่ากับ 1 หน่วย และเราสามารถหาความยาวของด้านที่เหลือของรูปสามเหลี่ยมได้จากสมการพีทาโกรัส คือ
ด้านตรงข้ามมุมฉาก c2 = ด้านประชิดมุมฉาก a2 + ด้านประชิดมุมฉาก b2
ดังนั้น ความยาวของด้านที่เหลือของรูปสามเหลี่ยมนี้คือ 12 = (1/2)2 + b2
b = √3/2
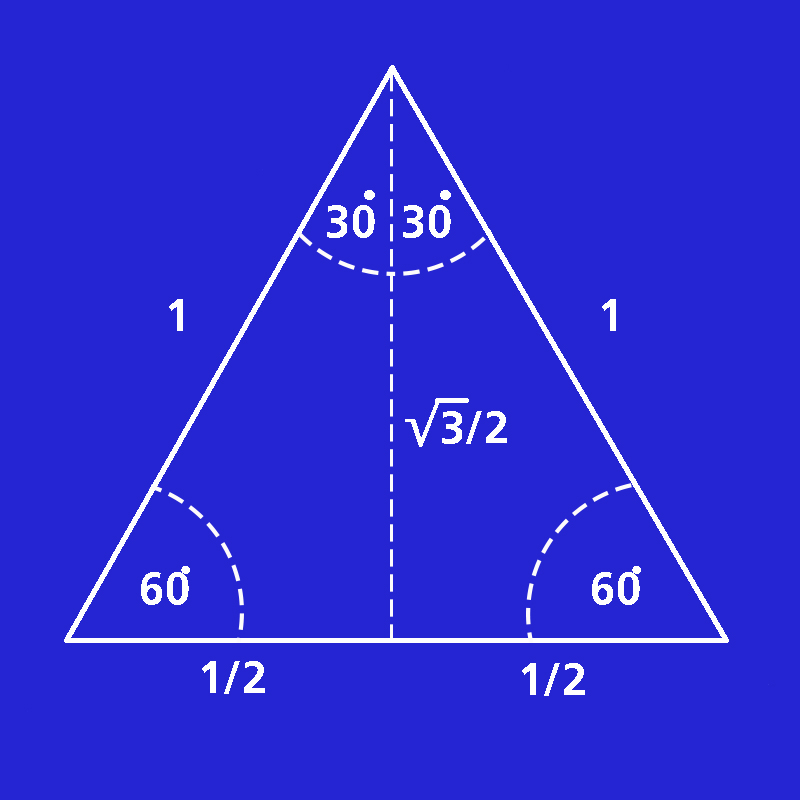
4. หาค่า sin cos tan ของมุม 30ํ และ 60ํ ได้ โดยดูจากภาพสามเหลี่ยมดังกล่าว
1. วาดรูปสามเหลี่ยมมุมฉากที่มีด้านประชิดมุมฉากยาวด้านละ 1 หน่วย จะได้สามเหลี่ยมที่มีมุมฉาก 1 มุม ส่วนมุมที่เหลือมีขนาด 45 ํ
2. หาความยาวของด้านที่เหลือ (ด้านตรงข้ามมุมฉาก) ของรูปสามเหลี่ยมได้จากสมการพีทาโกรัส ซึ่งจะได้ความยาวของด้านที่เหลือเป็น √2
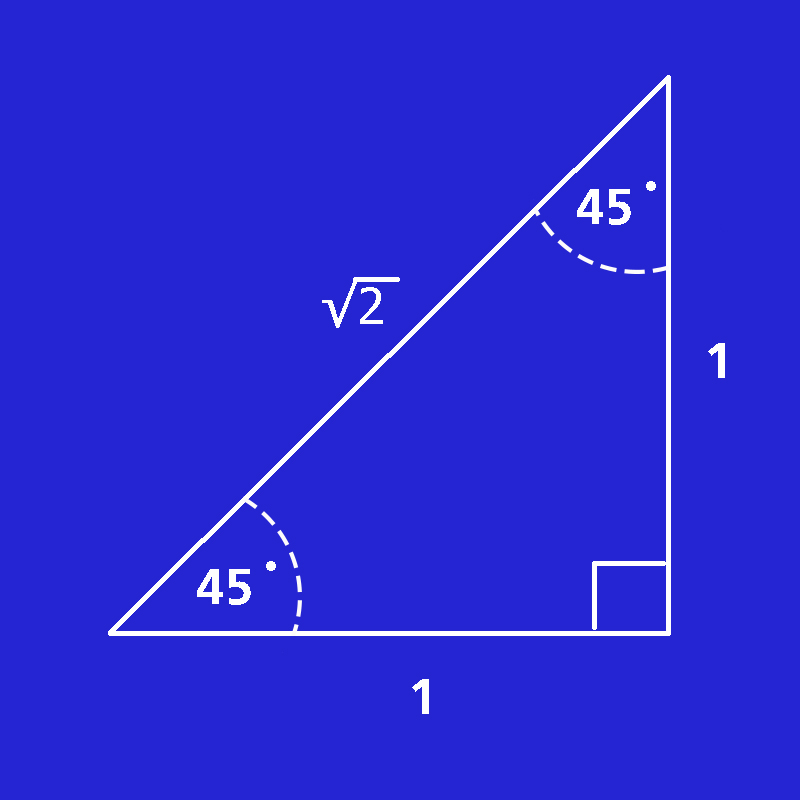
3. หาค่า sin cos tan ของมุม 45ํ ได้ โดยดูจากภาพสามเหลี่ยมดังกล่าว
1. วาดรูปสามเหลี่ยมมุมฉากที่มีด้านแต่ละด้านยาว 3 4 และ 5 หน่วย ตามลำดับ จะได้รูปสามเหลี่ยมมุมฉาก โดยอีกสองมุมที่เหลือมีขนาด 37ํ และ 53 ํ
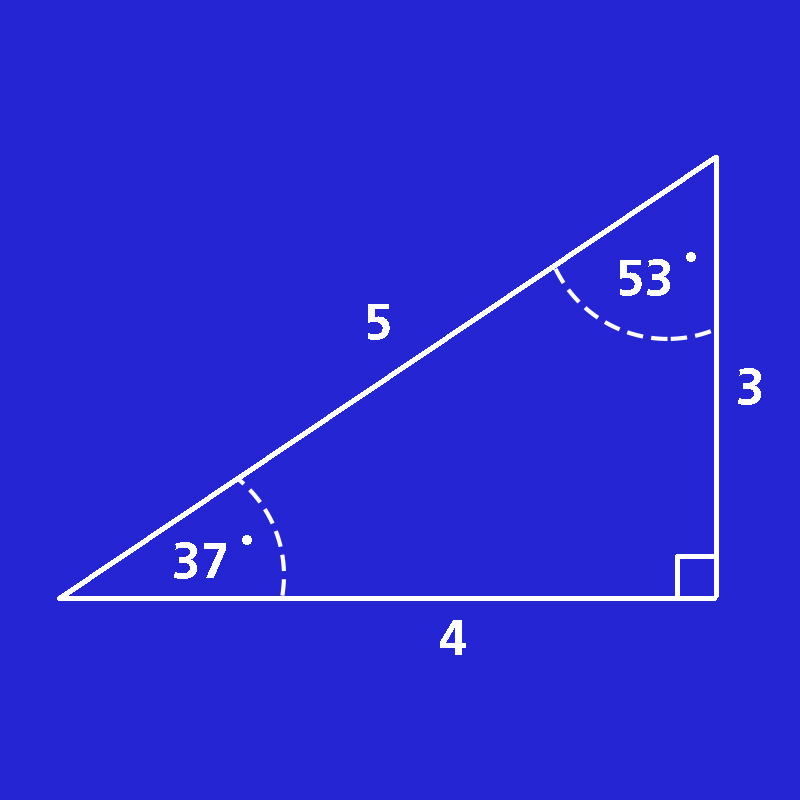
2. หาค่า sin cos tan ของมุม 37ํ และ 53 ํ ได้ โดยดูจากภาพสามเหลี่ยมดังกล่าว
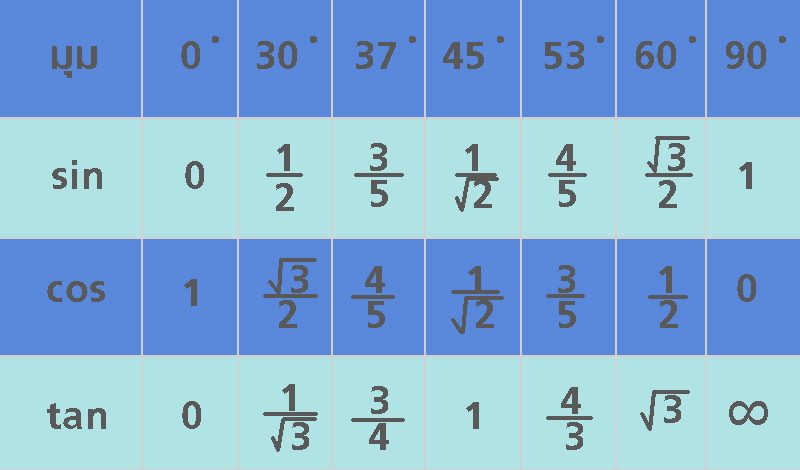
แต่ถ้าใครจำเก่งหรือชอบวิธีจำค่าไปใช้เลยมากกว่าก็ใช้ตารางนี้ได้เลยจ้า