 204,609 Views
204,609 Views
1. ค่าพาย (Pi, ¶) มีค่าเท่ากับ 22/7 หรือ 3.14... โดยเป็นค่าคงที่ทางคณิตศาสตร์ที่เกิดจากการนำความยาวของเส้นรอบวงหารด้วยเส้นผ่านศูนย์กลางของวงกลม มันเป็นค่าที่มีตัวเลขยาวต่อเนื่องกันไปอย่างไม่รู้จบ และไม่มีชุดตัวเลขใดที่ซ้ำกันเลย
2. สัญลักษณ์พาย (Pi, ¶) ถูกใช้กันทั่วไปในทางคณิตศาสตร์เมื่อ 250 ปีที่ผ่านมานี้เท่านั้น
3. William Jones เป็นคนแรกที่เสนอให้ใช้สัญลักษณ์พาย (Pi, ¶) ในปี 1706 แต่มันกลับได้รับความนิยมในเวลาต่อมา คือ ในปี 1737 ซึ่งเป็นยุคของ Leonhard Euler นักคณิตศาสตร์ชาวสวิส
4. ไม่เคยมีใครวัดค่าที่แท้จริงของเส้นรอบวงหรือพื้นที่วงกลมได้ เพราะไม่เคยมีใครทราบค่าที่แท้จริงของพายเลย มันเป็นตัวเลขมหัศจรรย์ที่สามารถคำนวณต่อไปได้เรื่อย ๆ อย่างไม่สิ้นสุด และยังเป็นตัวเลขที่สะเปะสะปะไม่ซ้ำกันอีกด้วย
5. มนุษย์รู้จักค่าพายมาเป็นเวลาเกือบ 4000 ปีแล้ว โดย 2000 ปีก่อนคริสตกาล ชาวบาบิโลเนียนกำหนดค่านี้ไว้ที่ 3 1/8 หรือ 3.125 ส่วนชาวอียิปต์โบราณใช้ค่าพายที่แตกต่างกันไปเล็กน้อยคือ 3 1/7 หรือ 3.143 ขณะที่ชาวจีนโบราณจะแทนค่าพายด้วยจำนวนเต็ม 3 แต่ในปี 1665 เซอร์ ไอแซก นิวตัน ได้คำนวณค่าพายไว้ที่ 16 ตำแหน่ง และปี 1719 นักคณิตศาสตร์ชาวฝรั่งเศสชื่อ Thomas Fantet de Lagny มีการคำนวณค่าพายไว้ที่ 127 ตำแหน่ง
6. William Shanks ใช้ความพยายามในการหาค่าพายโดยการคำนวณด้วยตนเอง และเขาก็ได้ค่าพายออกมาถึง 707 ตำแหน่ง แต่น่าเสียดายที่ค่าที่ได้มานั้น มีข้อผิดพลาดเกิดขึ้นตั้งแต่ตำแหน่งที่ 527 เป็นต้นไป ดังนั้น ตัวเลขค่าพายหลังจากตำแหน่งดังกล่าวจึงเป็นตัวเลขที่ผิดทั้งหมด
7. ในปี 2002 นักวิทยาศาสตร์ชาวญี่ปุ่น สามารถคำนวณค่าพายได้ถึง 1.24 ล้านล้านตัว จากการใช้คอมพิวเตอร์ที่เรียกว่า Hitachi SR 8000 ในการคำนวณ
8. ตัวเลข 144 ตัวแรกของค่าพาย (นับตั้งแต่หลังจุดทศนิยมเป็นต้นไป) บวกกันได้ 666 ความน่าสนใจอยู่ที่ตัวเลข 144 นั้นมีค่าเท่ากับ (6+6)x(6+6)
9. ในปี 2005 Chao Lu จากประเทศจีน ถูกบันทึกลงในกินเนสส์บุ๊คว่าเป็นผู้ที่สามารถจดจำตัวเลขค่าพายได้สูงสุดที่ 67,890 ตำแหน่ง แต่ในปี 2015 Rajveer Meena of Vellore จากประเทศอินเดีย ได้ทำลายสถิตินี้ลง และเขากลายเป็นผู้ที่จดจำค่าพายได้สูงสุดที่ 70,000 ตำแหน่ง นอกจากนี้ยังมีสถิติอย่างไม่เป็นทางการของ Akira Haraguchi ที่สามารถจดจำตัวเลขค่าพายได้ถึง 117,000 ตำแหน่งอีกด้วย (โอ้ แม่เจ้า!)
10. ¶ เป็นตัวอักษรตัวที่ 16 ในภาษากรีก ขณะที่ในภาษาอังกฤษ P ก็เป็นตัวอักษรตัวที่ 16 เช่นกัน
11. วันพายหรือ Pi day ตรงกับวันที่ 14 มีนาคมของทุก ๆ ปี ซึ่งนำมาจากตัวเลข 3.14 ซึ่งเป็นค่าของพาย มันเริ่มต้นขึ้นในปี 1988 โดยนักฟิสิกส์ที่ชื่อ Larry Shaw ซึ่งรู้จักกันในนาม Prince of Pi
12. นักวิทยาศาสตร์ที่ยิ่งใหญ่ที่สุดคนหนึ่งของโลก อัลเบิร์ต ไอน์สไตน์ เกิดในวันที่ 14 มีนาคม ซึ่งตรงกับวันพาย
13. คนส่วนใหญ่มักเข้าใจว่าวงกลมเป็นรูปทรงเรขาคณิตที่ไม่มีมุม แต่ในความเป็นจริงแล้ว วงกลมนั้นมีมุมที่นับไม่ถ้วนต่างหาก
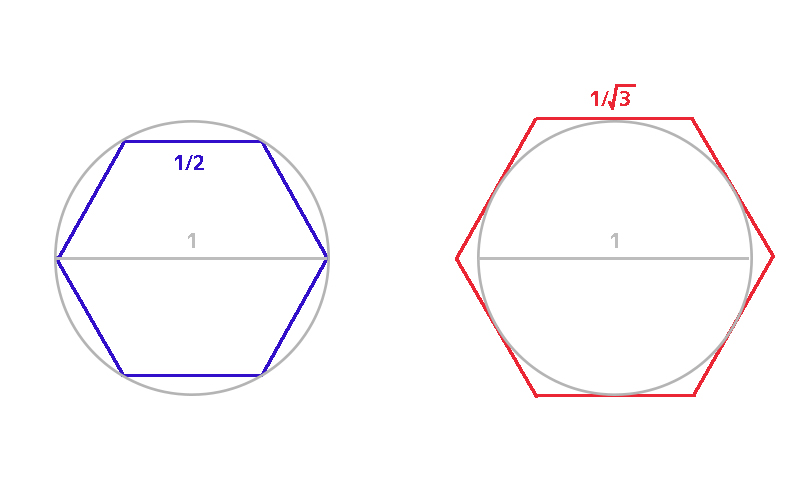
14. อาร์คิมีดีส นักคณิตศาสตร์ชาวกรีกที่มีชีวิตอยู่ในช่วง 287-212 ปีก่อนคริสตกาล เป็นบุคคลแรกที่เริ่มคำนวณค่าพายอย่างจริงจัง โดยการวาดรูปหกเหลี่ยมภายในและนอกวงกลมอย่างละรูป และวาดเส้นผ่านศูนย์กลางวงกลมขนาดเท่ากับ 1 หน่วย ดังนั้น จากสูตรการหาเส้นรอบวง 2¶r เส้นรอบวงของวงกลมนี้จะมีขนาดเท่ากับ พาย (¶) อาร์คิมีดีสสังเกตว่า ความยาวของแต่ละด้านของรูปหกเหลี่ยมสีฟ้าจะเป็นครึ่งหนึ่งของเส้นผ่านศูนย์กลาง เส้นรอบรูปหกเหลี่ยมสีฟ้าจึงเท่ากับ 6 × 1/2 = 3 และความยาวของแต่ละด้านของรูปหกเหลี่ยมสีแดงเป็น 1/√3 ของเส้นผ่านศูนย์กลาง เส้นรอบรูปหกเหลี่ยมสีแดงจึงเท่ากับ 6 × 1/√3 = 3.46 ดังนั้น ค่าพายจึงอยู่ระหว่าง 3 < ¶ < 3.46
เขาได้ทำเช่นเดียวกันนี้กับรูปหลายเหลี่ยมอื่น ๆ ตั้งแต่ 6 เหลี่ยม 12 เหลี่ยม 48 เหลี่ยม และ 96 เหลี่ยม ทำให้ได้ค่าพายอยู่ระหว่าง 3.1408 และ 3.1428 ซึ่งเป็นค่าพายที่ใกล้เคียงความเป็นไปได้มากที่สุด
15. นักโบราณคดีอียิปต์ให้ความสนใจเกี่ยวกับสัดส่วนของมหาพีระมิดแห่งกิซา เพราะมันมีส่วนเกี่ยวข้องกับค่าพาย โดยความสูงของพีระมิดสัมพันธ์กับเส้นรอบรูปของฐาน เช่นเดียวกับรัศมีของวงกลมที่สัมพันธ์กับเส้นรอบวง
บทความที่เกี่ยวข้อง
- รู้รอบโลก ตอน พาย ไม่ใช่ กล้วยกล้วย เกร็ดน่ารู้เกี่ยวกับจำนวนพาย
