
 4,043 Views
4,043 Views
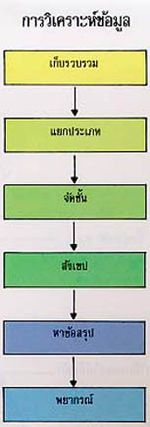
ข้อมูลที่ทำการเก็บรวบรวม โดยทั่วไปจะมีจำนวนมาก เมื่อได้ข้อมูลมาแล้ว ก็จะมีการดำเนินกับข้อมูลด้วยวิธีการต่างๆ เช่น การแยกประเภท การจัดชั้น การสังเขป การหาข้อสรุปเกี่ยวกับลักษณะต่างๆ ของข้อมูล การพิจารณาหาว่า ข้อมูลที่เก็บรวบรวมมาได้ มีความสัมพันธ์กับข้อมูลอื่นหรือไม่อย่างไร ตลอดจนอาจทำการพยากรณ์เหตุการณ์ในอนาคต จากข้อมูลที่เก็บรวบรวมได้ กระบวนการต่างๆ เหล่านี้เรียกว่า การวิเคราะห์ข้อมูล ซึ่งจะดำเนินการในรายละเอียดอย่างไร และ เพียงไรนั้น ขึ้นอยู่กับลักษณะของข้อมูล และ เรื่องที่ต้องการศึกษา ในบางกรณี การวิเคราะห์ข้อมูลก็ทำโดยใช้กราฟ ดังนั้น เมื่อพิจารณาให้ดีจะเห็นว่าบางขั้นตอนของการวิเคราะห์ข้อมูล เช่น การจัดชั้น หรือแยกประเภทของข้อมูล จะต้องเตรียมวางแผนพร้อมกันไปกับการเก็บรวบรวม และ การนำเสนอข้อมูล
เมื่อข้อมูลได้รับการวิเคราะห์แล้ว ขั้นสุดท้ายของการดำเนินการทางสถิติก็คือ การตีความหมายข้อมูลเหล่านั้น การตีความหมายก็คือ การพิจารณาหาว่า อะไรคือ ข้อสรุปที่ได้จากการวิเคราะห์ ตัวเลขที่ได้จากการวิเคราะห์ช่วยสนับสนุน หรือปฏิเสธสมมุติฐานที่ตั้งไว้เกี่ยวกับเรื่องนั้นๆ และ ตัวเลขที่ได้จากการวิเคราะห์ บอกอะไรบางอย่างใหม่ๆ แก่เราบ้าง
การตีความหมายข้อมูลเป็นเรื่องที่ทำได้ไม่ง่ายนัก เนื่องด้วยความรู้ และ เอกสารเกี่ยวกับเรื่องที่เกี่ยวข้องมักมีจำกัด ดังนั้น การตีความหมายข้อมูล จึงไม่ควรสรุปลงไปอย่างแน่นอนตายตัวว่า ต้องเป็นอย่างนั้นอย่างนี้ นอกจากนั้นเหตุผลอีกประการหนึ่งที่สนับสนุนการกระทำดังกล่าวนี้ ก็คือ ตัวข้อมูลเอง ได้เคยกล่าวไว้แล้วว่า ข้อมูลประกอบด้วยข้อเท็จ และ ข้อจริง มิใช่ข้อจริงล้วนๆ และ ตัวเลขที่ได้จากการวิเคราะห์ ก็เป็นเพียงค่าประมาณ ดังนั้นการตีความหมายข้อมูลโดยการสรุปอย่างแน่นอนตายตัว จึงมีโอกาสผิดพลาดได้ง่ายมาก
อย่างไรก็ตาม การตีความหมายที่ดี ขึ้นอยู่กับหลักเกณฑ์ ๔ ประการ ดังต่อไปนี้
๑. มีความตั้งใจแน่วแน่ที่จะค้นหาความจริงทุกอย่างที่ซ่อนเร้นอยู่ในข้อมูล
๒. มีความรู้ความเข้าใจอย่างกว้างขวางในเหตุการณ์หรือเรื่องที่กำลังศึกษา
๓. มีความคิดที่เป็นระเบียบ และ มีเหตุผลในการทำงาน
๔. มีความสามารถในการใช้ถ้อยคำที่ชัดเจน ทำให้อ่านเข้าใจได้ง่าย
กระบวนการต่างๆ ของการวิเคราะห์ข้อมูล แยกกล่าวเป็นข้อๆ ได้ดังต่อไปนี้
๑. การแยกประเภทข้อมูล (Classification)
ข้อมูลที่เก็บรวบรวมมาได้ อาจมีมากประเภท หรือ น้อยประเภท แล้วแต่เรื่องที่ต้องการศึกษา ตัวอย่างข้อมูลเกี่ยวกับชาวนา เช่น จำนวนชาวนา เนื้อที่เพาะปลูก และ ผลิตผลของข้าว รายได้ เป็นต้น ข้อมูลแต่ละประเภทเหล่านี้อาจจำแนกเป็นชนิดย่อยออกไปอีก ทั้งนี้เพื่อจะได้ศึกษาในรายละเอียดปลีกย่อยต่างๆ ให้มากขึ้นตามความต้องการ เช่น จำนวนชาวนา อาจจำแนกตามเพศ อายุ และ ชั้นการศึกษา เนื้อที่เพาะปลูก และ ผลิตผลข้าวอาจจำแนกออกเป็นข้าวเจ้า และ ข้าวเหนียว รายได้ อาจจำแนกตามแหล่งที่มา เช่น เงินที่ได้จากการขายข้าว ค่าเช่าที่นา ค่าแรงงานรับจ้าง เป็นต้น

การแยกประเภทข้อมูล อาจเป็นขั้นตอนที่พอเพียงสำหรับการวิเคราะห์ข้อมูลบางอย่าง ซึ่งไม่ต้องการศึกษาข้อมูลในขั้นลึกซึ้งนัก แต่สำหรับการศึกษาบางอย่าง การแยกประเภทข้อมูลเป็นเพียงขั้นเตรียมงานเท่านั้น ซึ่งในประการหลังนี้ ลักษณะต่างๆ ของข้อมูลทั้งที่เป็นรายข้อมูล และ ในส่วนรวมจะต้องได้รับการพิจารณา และ ศึกษาอย่างละเอียดละออ
๒. การสังเขปข้อมูล (Condensation)
ข้อมูลที่เก็บรวบรวมมาได้ในขั้นแรกจะอยู่ในสภาพที่ไม่เป็นระเบียบเรียบร้อย ยังไม่สามารถทำการหาข้อสรุปของลักษณะต่างๆ ของข้อมูลได้ ข้อมูลที่อยู่ในรูปเช่นนี้มีชื่อเรียกว่า "ข้อมูลดิบ" (Raw data) ดังนั้น เพื่อให้ข้อมูลอยู่ในสภาพพร้อม ที่จะสามารถหาข้อสรุป หรือ ทำการวิเคราะห์โดยวิธีอื่นๆ ได้ จึงอาจดำเนินการสังเขปข้อมูลดิบ หรือ จัดข้อมูลดิบทั้งสิ้น ให้อยู่ในรูปแบบใหม่ ซึ่งเป็นระเบียบเรียบร้อย และ มีขนาดกะทัดรัดสะดวกต่อการดำเนินการวิเคราะห์ในขั้นต่อไป การสังเขปข้อมูลตามที่กล่าวมานี้เรียกว่า "การแจกแจงความถี่" (Frequency distribution)

ในกรณีที่ข้อมูลมีจำนวนไม่มากนัก การแจกแจงความถี่อาจแสดงเป็นรายข้อมูลที่เก็บรวบรวมมาได้ พร้อมทั้งความถี่ หรือ จำนวนที่ซ้ำๆ กันของข้อมูลตัวนั้นๆ
ตัวอย่าง นักเรียน ๔๐ คน สอบไล่วิชาเลขคณิตได้คะแนน ดังต่อไปนี้
| ๑๕ | ๒๓ | ๒๕ | ๒๗ | ๑๙ | ๒๐ | ๑๙ | ๑๗ |
| ๑๘ | ๒๔ | ๒๓ | ๒๖ | ๒๙ | ๒๕ | ๒๑ | ๒๓ |
| ๒๕ | ๒๕ | ๒๕ | ๒๕ | ๒๔ | ๑๗ | ๒๐ | ๒๕ |
| ๒๘ | ๒๖ | ๒๕ | ๒๐ | ๒๒ | ๒๒ | ๒๖ | ๒๖ |
| ๒๐ | ๒๒ | ๒๒ | ๒๑ | ๑๙ | ๒๗ | ๒๔ | ๒๔ |
ข้อมูลข้างต้นนี้ เรียกว่า ข้อมูลดิบ เมื่อแจกแจงความถี่เป็นรายข้อมูลจะได้ดังนี้
| คะแนน | ความถี่ |
| ๑๕ | ๑ |
| ๑๖ | - |
| ๑๗ | ๒ |
| ๑๘ | ๑ |
| ๑๙ | ๓ |
| ๒๐ | ๔ |
| ๒๑ | ๒ |
| ๒๒ | ๔ |
| ๒๓ | ๓ |
| ๒๔ | ๕ |
| ๒๕ | ๗ |
| ๒๖ | ๔ |
| ๒๗ | ๒ |
| ๒๘ | ๑ |
| ๒๙ | ๑ |
| รวม | ๔๐ |
การแจกแจงความถี่ที่ได้แสดงไว้ข้างบนนี้ ถ้าข้อมูลมีจำนวนมาก ตารางดังกล่าวจะยากมาก ทำให้ต้องเสียเนื้อที่กระดาษ และ ไม่สะดวก ที่จะทำการวิเคราะห์ในขั้นต่อไป นอกจากนี้ถ้าจะพิจารณาในด้านการกระจายของข้อมูลว่า ข้อมูลส่วนใหญ่มีค่าระหว่างเท่าไรถึงเท่าไร หรือ รูปลักษณะการกระจายข้อมูลเป็นอย่างไร ก็จะไม่สามารถแลเห็นรูปลักษณะของการกระจายได้ชัดเจน ดังนั้น จึงอาจจะจัดทำการแจกแจงความถี่ของข้อมูลให้อยู่ในรูปใหม่ ซึ่งมีลักษณะอัดแน่นกว่าตารางข้างต้น กล่าวคือ จัดข้อมูลให้รวมอยู่เป็นกลุ่มๆ แล้วดูว่าข้อมูลค่าต่างๆ อยู่ในกลุ่มหรือชั้นใดบ้าง ให้นับจำนวนข้อมูลเหล่านั้นว่า อยู่ในชั้นใดเป็นจำนวนเท่าใด จำนวนข้อมูลในแต่ละชั้นเรียกว่า ความถี่
อย่างไรก็ตาม ถ้าจัดกลุ่มข้อมูลแต่ละกลุ่มให้มีขนาดใหญ่มาก จำนวนกลุ่ม หรือ จำนวนชั้นก็จะมีน้อย และ จำนวนข้อมูลในแต่ละกลุ่ม ก็จะอัดกันแน่นมากเกินไป ทำให้ไม่สามารถแลเห็นลักษณะการกระจายของข้อมูลได้ดี แต่ถ้าหากจัดแต่ละกลุ่มให้มีขนาดเล็กมาก จำนวนกลุ่ม หรือ จำนวนชั้นก็จะมีมาก ซึ่งจะทำให้การกระจายของข้อมูลมีลักษณะแผ่กว้างมากเกินไป ไม่ช่วยให้แลเห็นลักษณะการกระจายที่ดี ดังนั้น การแจกแจงความถี่แบบจัดข้อมูลให้เป็นกลุ่มๆ นี้ จึงต้องให้แต่ละกลุ่มมีขนาดโตพอดี ที่จะทำให้แลเห็นลักษณะการกระจายของข้อมูลได้อย่างเด่นชัด กล่าวคือ ข้อมูลในกลุ่มจะต้องไม่อัดแน่นมากเกินไป และ ก็ต้องไม่แผ่กระจายมากจนเกินไปด้วย
ตารางข้างล่างนี้ เป็นตารางการแจกแจงความถี่ที่ได้จัดข้อมูลเป็นกลุ่มๆ โดยได้ใช้ข้อมูลที่ให้ไว้ข้างต้น ตารางดังกล่าวนี้ เป็นแบบอย่างของตารางทั่วไป ที่ใช้ในการวิเคราะห์ข้อมูล
| คะแนน | ความถี่ |
| ๑๕ - ๑๗ | ๓ |
| ๑๘ - ๒๐ | ๘ |
| ๒๑ - ๒๓ | ๙ |
| ๒๔ - ๒๖ | ๑๖ |
| ๒๗ - ๒๙ | ๔ |
| รวม | ๔๐ |
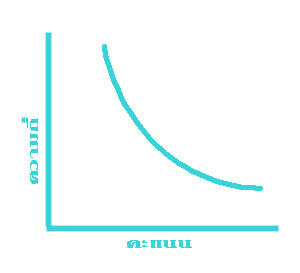
ข้อมูลแต่ละชุดที่เก็บรวบรวมมาได้ อาจมีรูปลักษณะของการแจกแจงความถี่ไม่เหมือนกัน ลักษณะการแจกแจงความถี่ที่พบมากที่สุด ได้แก่ข้อมูลที่มีค่ากลางๆ มีจำนวนมาก ส่วนข้อมูลที่มีค่าสูง และ ที่มีค่าต่ำมีจำนวนน้อย ถ้านำข้อมูลประเภทนี้มาเขียนกราฟจะได้รูปโค้ง ดังแสดงไว้ในรูปที่ ๑ รูปที่ ๒ และรูปที่ ๓ ข้างล่างนี้
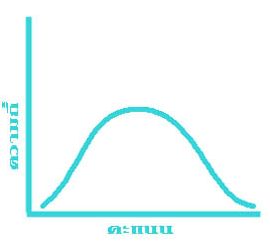
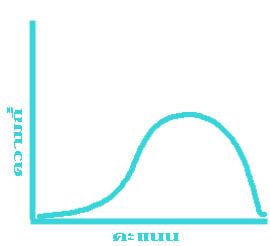
รูปที่ ๑ แสดงให้เห็นว่า ข้อมูลที่มีค่ามาก และ ข้อมูลที่มีค่าน้อย เมื่อนับจากข้อมูลที่มีค่ากลางจะมีจำนวนเท่าๆ กัน ดูจากรูปจะเห็นว่าปลายทั้งสองข้างของโค้งมีลักษณะสมมาตร (Symmetrical) รูปการแจกแจงความถี่ของข้อมูลที่มีลักษณะเช่นนี้ เรียกว่า โค้งปกติ (Normal curve) หรือ โค้งรูประฆังคว่ำ
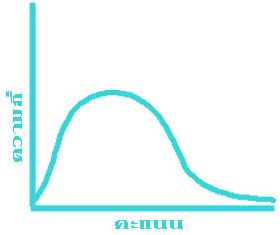
สำหรับรูปที่ ๒ และ รูปที่ ๓ นั้น เป็นการแจกแจงความถี่ของข้อมูลที่มีลักษณะที่เรียกว่า มีความเบ้ (Skewness) นั่นคือ ข้อมูลค่าน้อยมีจำนวนมากกว่าข้อมูลที่มีค่ามาก หรือ ที่เรียกว่า เบ้ไปทางบวก (Positively skewed) ซึ่งได้แก่รูปที่ ๒ และข้อมูลค่ามาก มีจำนวนมากกว่าข้อมูลที่มีค่าน้อย หรือ ที่เรียกว่า เบ้ไปทางลบ (Negatively skewed) ซึ่งได้แก่ รูปที่ ๓
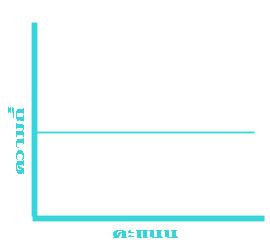
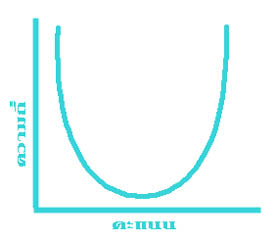
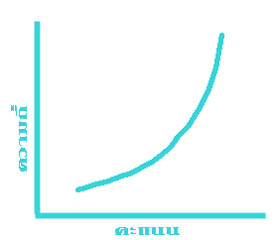
การแจกแจงความถี่ของข้อมูลลักษณะอื่นที่จะยกมาให้ดู นอกจากนี้ก็มีรูปสี่เหลี่ยมผืนผ้า (รูปที่ ๔) รูปตัว U (รูปที่ ๕) รูปตัว J (รูปที่ ๖) และ รูปตัว J กลับ (รูปที่ ๗) ดังแสดงไว้ข้างล่างนี้
๓. การหาข้อสรุปเกี่ยวกับลักษณะต่างๆ ของข้อมูล (Summarization)
ข้อมูลแต่ละชุดที่เก็บรวบรวมมาได้ อาจมีลักษณะการแจกแจงความถี่แตกต่างกันไปดังได้กล่าวแล้วในข้อ ๒ ในการวิเคราะห์ข้อมูล เราจำเป็นต้องศึกษาอย่างละเอียดละออว่า ข้อมูลชุดนั้นๆ บอกอะไรแก่เราบ้าง เช่น สมมุติว่า มีข้อมูลเกี่ยวกับรายได้ต่อปีของคนจำนวนหนึ่ง ซึ่งเป็นตัวอย่างของประชากรทั้งประเทศ สิ่งต่างๆ ที่อาจต้องการทราบก็คือ ประชากรมีรายได้ต่อปีเฉลี่ยคนละเท่าไร รายได้ของคนมั่งมี และ คนยากจนแตกต่างกันมากหรือไม่ และ ถ้าคนส่วนใหญ่ค่อนข้างยากจน คนเหล่านี้มีมากเพียงไร ค่าเหล่านี้คือ ค่าซึ่งบอกลักษณะต่างๆ ของข้อมูล ซึ่งเป็นค่าสถิติอย่างหนึ่ง และ สามารถคำนวณหาได้
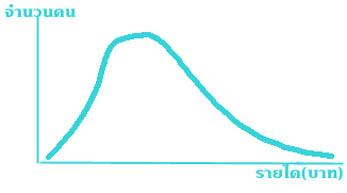
อันที่จริงค่าต่างๆ เหล่านี้ พอจะทราบได้อย่างคร่าวๆ จากลักษณะการแจกแจงความถี่ของข้อมูล สมมุติว่า รูปที่ ๘ ได้จากการแจกแจงความถี่ของรายได้ต่อปีของประชากรตามที่กล่าวข้างต้น สิ่งที่ทราบได้อย่างคร่าวๆ จากรูปดังกล่าวก็คือ ประชากรที่มีรายได้ปานกลางค่อนไปทางข้างต่ำมีจำนวนมาก ส่วนประชากรที่มีรายได้ต่ำมาก หรือ สูงมากมีจำนวนน้อย นอกจากนั้นช่องว่างระหว่างคนร่ำรวย และ คนยากจนกว้างมาก ทั้งนี้เพราะปลายทั้งสองข้างของรูปโค้งห่างกันมาก อย่างไรก็ตามในทางสถิติ ข้อสรุปที่มิใช่ตัวเลขมีความหมายน้อย และ ไม่สามารถจะนำไปใช้ประโยชน์ในขั้นต่อไปได้ ดังนั้น ข้อสรุปทั้งหลายาของข้อมูลจึงต้องแสดงออกเป็นตัวเลข
เนื่องจากการแจกแจงความถี่ของข้อมูลที่พบส่วนมาก มีลักษณะเป็นโค้งรูประฆัง กล่าวคือ ตรงกลางป่อง และ โค้งจะลาดลงทั้งสองข้าง ดังนั้นการหาค่าที่บอกลักษณะสำคัญของข้อมูลที่มีการกระจายลักษณะนี้ ได้แก่ การหาค่ากลาง และ การหาค่าการกระจายของข้อมูล ซึ่งจะได้กล่าวเป็นเรื่องๆ ต่อไป
๓.๑ การหาค่ากลางของข้อมูล
ค่ากลางของข้อมูลซึ่งมีที่ใช้มากได้แก่ มัชฌิมเลขคณิต (Arithmetic Mean) มัธยฐาน (Median) และ ฐานนิยม (Mode)
ก) มัชฌิมเลขคณิตของข้อมูลชุดใดๆ คือ ค่าเฉลี่ยของข้อมูลชุดนั้น ซึ่งอาจเขียนให้อยู่ในรูปสูตรได้ดังนี้

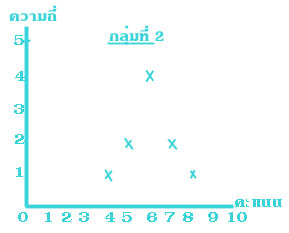
เนื่องจากพิสัยเป็นสถิติที่ใช้วัดการกระจายได้อย่างคร่าวๆ เท่านั้น ดังนั้นจึงมักไม่เป็นที่นิยมใช้กัน
สถิติวัดการกระจายที่สำคัญ และ ใช้กันทั่วไป คือ ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) ซึ่งหาได้จากการเอาผลต่างระหว่างข้อมูลแต่ละค่า และ มัชฌิมเลขคณิตของข้อมูลนั้นมายกกำลังสอง แล้วทำการถัวเฉลี่ยค่ากำลังสองเหล่านั้น จากนั้นจึงถอดกรณฑ์ที่สองของค่าเฉลี่ยที่ได้
จากข้อมูลกลุ่มที่ ๒ หาค่าส่วนเบี่ยงเบนมาตรฐานได้ดังนี้
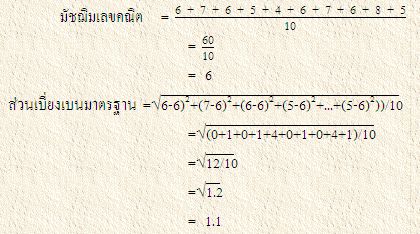
ค่าที่ได้จากการวัดการกระจายของข้อมูลเป็นสถิติสำคัญที่นำไปใช้ประโยชน์อย่างกว้างขวาง ค่าปานกลางเพียงอย่างเดียว ไม่สามารถใช้บรรยายลักษณะสำคัญของข้อมูลทั้งกลุ่มได้เพียงพอ เช่นคนกลุ่มหนึ่งมีรายได้เฉลี่ยค่อนข้างสูง แต่มิได้หมายความว่า ทุกคนในกลุ่มนั้นจะต้องมีรายได้สูงไปด้วย อาจจะมีบางคน ซึ่งมีรายได้สูงมากและต่ำมากรวมอยู่ด้วย หรือ ทั้งกลุ่มอาจจะมีรายได้ไล่เลี่ยกัน ไม่แตกต่างกันมากนักก็เป็นได้ ลักษณะเช่นที่ว่านี้จะต้องดูจากการกระจายของ ข้อมูลซึ่งบางกลุ่มก็มีการกระจายมาก บางกลุ่มก็มีน้อย
นอกจากนี้ประโยชน์ที่ได้จากการกระจายของข้อมูล ก็คือการนำไปใช้ในการควบคุมคุณภาพของผลิตภัณฑ์บางอย่าง โดยพิจารณากำหนดว่า สิ่งของที่ผลิตได้ อาจจะเบี่ยงเบนไปจากคุณภาพมาตรฐานได้บ้าง แต่ต้องไม่เกินเท่าไร และ ทำนองเดียวกัน ในด้านของการพยากรณ์ก็จะสามารถใช้ค่าการกระจายเป็นตัวกำหนดได้ว่า การพยากรณ์นั้นๆ จะเชื่อถือได้มากน้อยเพียงไร และ ถ้าจะพยากรณ์คลาดเคลื่อนจากความจริงไปบ้างจะไม่มากหรือน้อยกว่าเท่าไร เป็นต้น
๔. แนวโน้มของข้อมูล (Trend)
ข้อมูลบางชนิดแสดงถึงเหตุการณ์ที่เกิดขึ้นเป็นรายคาบเวลา เช่น ปริมาณสินค้าส่งออกเป็นรายปี จำนวนอุบัติเหตุรถยนต์บนท้องถนนเป็นรายสัปดาห์ ปริมาณน้ำฝนที่ตกเป็นรายเดือน เป็นต้น ข้อมูลประเภทนี้เรียกว่า ข้อมูลอนุกรมเวลา (Time-series data)
ถ้านำข้อมูลประเภทนี้ที่เกิดขึ้นในช่วงเวลาหนึ่งซึ่งยาวนานพอสมควรมาลงจุดจะได้เส้นกราฟ ซึ่งมีลักษณะโดยส่วนรวมอาจชันขึ้น หรือ ลาดลง หรือ มีทั้งชันขึ้นหรือลาดลงในช่วงเวลาหนึ่งเช่นในรอบ ๑ ปี เป็นต้น ลักษณะโดยส่วนรวมที่ชันขึ้น หรือ ลาดลงของเส้นกราฟในช่วงเวลายาวนานนี้ เรียกว่า แนวโน้มของข้อมูล
วิธีการหาแนวโน้มของข้อมูลอาจแบ่งได้เป็น ๒ วิธีใหญ่ๆ คือ
๑) วิธีการกะประมาณ ซึ่งโดยมากใช้การลากเส้นอย่างอิสระ (Freehandmethod)
๒) วิธีการคำนวณที่นิยมใช้ก็มีการถัวเฉลี่ยเคลื่อนที่ (Moving averagemethod) และ วิธีกำลังสองน้อยที่สุด (Least squares method) ซึ่งวิธีหลังนี้จะได้แนวโน้มอยู่ในรูปของสมการ
๔.๑ การลากเส้นอย่างอิสระ
การสร้างแนวโน้มด้วยวิธีนี้ คือ การลากเส้น ซึ่งเป็นแนวเรียบผ่านไปในระหว่างเส้นกราฟของข้อมูล ซึ่งปกติจะมีบางตอนหักเหขึ้น และ บางตอนหักเหลง เส้นซึ่งเป็นแนวเรียบนี้แสดงถึงความเป็นไปโดยส่วนรวมในระยะยาวของเหตุการณ์ทั้งหมดที่เกิดขึ้น ซึ่งเราเรียกว่า แนวโน้มของข้อมูล การลากเส้นอย่างอิสระนี้ไม่มีกฎเกณฑ์ใดๆ ทั้งสิ้น นอกจากคอยระมัดระวังให้แนวโน้ม แสดงถึงเหตุการณ์ที่เกิดขึ้นในระยะยาวได้ถูกต้องเท่านั้น ดังแสดงด้วยรูปข้างล่างนี้
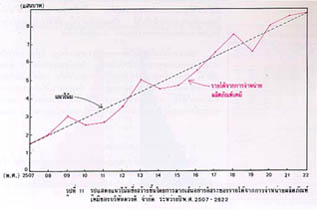
๔.๒ การถัวเฉลี่ยเคลื่อนที่
สมมุติว่า มีข้อมูลจำนวนหนึ่ง ซึ่งเก็บรวบรวมไว้เป็นรายเดือน ถ้าเราหาค่ามัชฌิมเลขคณิตของข้อมูลในช่วงเวลาหนึ่ง เช่น ในรอบ ๓ เดือน เป็นต้น แล้วจดค่านี้ไว้ จากนั้นก็เลื่อนช่วงเวลา ๓ เดือนนี้ต่อไป โดยตัดข้อมูลตัวแรกออก และ เพิ่มข้อมูลตัวที่ ๔ เข้ามา แล้วก็หามัชฌิมเลขคณิตของช่วงเวลาดังกล่าวนี้อีก และ จดค่าที่คำนวณได้ไว้ ทำเช่นนี้เรื่อยๆ ไป ก็จะได้ข้อมูลชุดใหม่ ซึ่งเป็นค่ามัชฌิมเลขคณิตของข้อมูลทุกๆ ๓ เดือนต่อเนื่องกัน วิธีการเช่นนี้เรียกว่า การถัวเฉลี่ยเคลื่อนที่ ๓ เดือน ในข้อมูลบางชุด อาจทำการถัวเฉลี่ยเคลื่อนที่ทุก ๕ เดือน หรือทุก ๓ ปี หรือ ทุก ๕ ปีก็ได้ ทั้งนี้ขึ้นอยู่กับชนิด และ ลักษณะของข้อมูล
เมื่อนำค่ามัชฌิมเลขคณิตเคลื่อนที่ที่ได้นี้มาลงจุด แล้วโยงจุดต่างๆ เหล่านี้ ก็จะได้เส้นซึ่งแสดงแนวโน้มของข้อมูลเป็นรายเดือน
ตารางข้างล่างนี้เป็นการคำนวณหาแนวโน้มของราคาเฉลี่ยต่อเกวียนของ ข้าวเปลือกเจ้าชั้นพิเศษ ๑๐๐% ที่ซื้อขายกันในตลาดกรุงเทพมหานคร ระหว่าง เดือน มกราคม ถึง ธันวาคม ๒๕๒๒ โดยวิธีการถัวเฉลี่ยเคลื่อนที่ ๓ เดือน
(ตัวเลขมีหน่วยเป็นบาท)
|
| ราคาเฉลี่ยต่อเกวียน | ผลรวมเคลื่อนที่ | มัชฌิมเลขคณิต |
| มกราคม กุมภาพันธ์ มีนาคม เมษายน พฤษภาคม มิถุนายน กรกฎาคม สิงหาคม กันยายน ตุลาคม พฤศจิกายน ธันวาคม | 2,520 2,581 2,660 2,736 2,757 2,831 2,774 2,916 3,171 3,252 3,184 3,237 | - 7,761 7,977 8,153 8,324 8,362 8,521 8,861 9,339 9,607 9,673 - | - 2,587.0 2,659.0 2,717.7 2,774.7 2,787.3 2,840.3 2,953.7 3,113.0 3,202.3 3,224.3 - |
ที่มา :รายงานเศรษฐกิจ ธนาคารกรุงไทยจำกัด มิถุนายน ๒๕๒๒
เมื่อนำเอาค่ามัชฌิมเลขคณิตเคลื่อนที่ 3 เดือนมาลงจุด จะได้แนวโน้มของราคาเฉลี่ยต่อเกวียนของข้าวเปลือกเจ้าชั้นพิเศษ ๑๐๐% ในรอบปี พ.ศ. ๒๕๒๒ ดังแสดงในรูปข้างล่างนี้
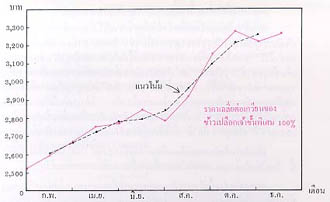
อันที่จริงเส้นที่ได้นี้ จะไม่ถือว่าเป็นแนวโน้มก็ได้ เพราะมิได้แสดงถึงแนวโน้มของเหตุการณ์ที่เกิดขึ้นในระยะยาวอย่างแท้จริง หากแต่เป็นเส้นซึ่งช่วยลดการกระเพื่อมขึ้นลงของเส้นกราฟอันเกิดจากข้อมูลเดิมให้เรียบขึ้นเท่านั้น

แนวโน้มของข้อมูลเป็นเครื่องมืออย่างหนึ่งที่ใช้ในการพยากรณ์ ส่วนที่ต่อจากปลายแนวโน้มออกไปคือ คำพยากรณ์ ดังนั้น ถ้าทำการวิเคราะห์ข้อมูล ด้วยการศึกษาแนวโน้ม อย่างละเอียดลออทุกแง่ทุกมุมแล้ว จะช่วยเพิ่มความแม่นยำ ให้แก่การพยากรณ์ยิ่งขึ้น
๕. การพยากรณ์ทางสถิติ
เมื่อเอ่ยคำว่า พยากรณ์ บางคนอาจนึกถึงโหรหรือหมอดู เพราะการพยากรณ์ก็คือ การทำนายล่วงหน้า ซึ่งมักเป็นงานของโหร แต่การพยากรณ์มิใช่งานผูกขาดของโหร ใครๆ ก็พยากรณ์ได้ ต่างกันก็แต่ว่าหลักเกณฑ์ และ วิธีการที่ใช้ในการพยากรณ์ แตกต่างกันอย่างไรเท่านั้น การพยากรณ์ที่ทำกันโดยทั่วไปมีอยู่ ๓ วิธี คือ
๕.๑ พยากรณ์โดยอาศัยประสบการณ์ และ ความชำนาญ
วิธีนี้นิยมใช้กันมาก เนื่องจากไม่ต้องมีหลักเกณฑ์ที่แน่นอนอะไร เพียงแต่อาศัยประสบการณ์ และ ความรู้ความชำนาญทางด้านนี้ ตลอดจนเข้าใจแจ่มแจ้งในปัญหาของเรื่องที่จะพยากรณ์ เช่น สมาคมผู้ค้าข้าวโพดทำการประเมินผลผลิตข้าวโพดประจำปี โดยการส่งคณะเจ้าหน้าที่ออกไปตระเวนดูสภาพของต้นข้าวโพด ในท้องที่ที่มีการปลูกข้าวโพดมากทั่วประเทศ แล้วเปรียบเทียบว่า สภาพต้นข้าวโพดในปีนี้ดีหรือเลวกว่าปีที่แล้วเพียงไร ปลูกในเนื้อที่มากขึ้น หรือลดลง จากนั้นก็พยากรณ์ผลผลิตข้าวโพด โดยใช้ผลผลิตของปีที่แล้วเป็นหลักว่า ควรเพิ่ม หรือ ลดลงเท่าไร
อย่างไรก็ตาม การพยากรณ์ด้วยวิธีนี้ สามารถนำไปใช้ได้ในกรณีที่มีการดำเนินงานในขอบเขตขนาดเล็กเท่านั้น อนึ่ง การพยากรณ์ด้วยวิธีนี้ แม้จะเป็นวิธีที่ง่าย แต่ก็มีโอกาสผิดพลาดได้มาก โดยเฉพาะอย่างยิ่งถ้าผู้พยากรณ์ไม่มีประสบการณ์ หรือ ขาดความรู้ความชำนาญเกี่ยวกับเรื่องที่จำทำการพยากรณ์
๕.๒ พยากรณ์โดยอาศัยเหตุการณ์ และ หลักฐานบางอย่าง
การพยากรณ์ด้วยวิธีนี้ มักมีการอภิปรายประกอบหลักฐานกันอย่างกว้างขวางแล้วสรุปหาข้อยุติ หลักฐานเหล่านี้อาจเป็นหลักฐานทางนิติศาสตร์ ทางการเมือง ทางเศรษฐกิจ และ สังคม ตัวอย่างเช่น เมื่อสงครามโลกครั้งที่สองได้สิ้นสุดลง ก็มีผู้พยากรณ์ว่า จะเกิดภาวะข้าวยากหมากแพง โจรผู้ร้ายชุกชุม เช่นเดียวกับที่เคยเกิดมาแล้ว ภายหลังสงครามโลกครั้งที่หนึ่ง เป็นต้น การพยากรณ์แบบนี้อาจกล่าวในเชิงคณิตศาสตร์ได้ว่า ตั้งอยู่บนรากฐานของ"ตัวแปรที่วัดค่าไม่ได้"
๕.๓ การพยากรณ์ทางสถิติ
เป็นการพยากรณ์โดยใช้ข้อมูลสถิติประเภทที่เรียกว่า ข้อมูลอนุกรมเวลาเป็นเครื่องมือ การพยากรณ์โดยวิธีนี้ จะต้องศึกษาถึงพฤติการณ์ของเรื่องนั้นๆ ที่เกิดขึ้นในอดีตว่า มีลักษณะอย่างไรเสียก่อน แล้วจึงทำการพยากรณ์ ข้อมูลอนุกรมเวลาจะบอกให้ทราบถึงพฤติการณ์นั้นๆ ตัวอย่างของการพยากรณ์ทางสถิติในเรื่องที่เกี่ยวกับเศรษฐกิจ และ ธุรกิจ ได้แก่ การพยาการณ์จำนวนประชากรของประเทศ การพยากรณ์ผลผลิตทางการเกษตร ปริมาณการขาย ระดับราคาสินค้า ฯลฯ เป็นต้น
การพยากรณ์ทางสถิติจะทำได้ต่อเมื่อพฤติการณ์ที่เกิดขึ้นในอดีตมีความแปรผันตามปกติ เช่น แต่ละปีที่ผ่านไป จำนวนประชากรของโลกมีแนวโน้มเพิ่มขึ้นเรื่อยๆ หรือ อัตราการตายของเด็กอายุต่ำกว่า ๑ ปี มีแนวโน้มลดลงอย่างสม่ำเสมอ หรือสินค้าเครื่องกันหนาวจะขายได้มากในฤดูหนาว แต่จะขายได้น้อยในฤดูอื่นๆ เป็นต้น แต่ถ้าพฤติการณ์ที่เกิดขึ้นในอดีต มีความแปรผันผิดปกติ เช่น สินค้าเครื่องกันหนาว แทนที่จะขายได้น้อยในฤดูอื่นนอกจากฤดูหนาวเป็นประจำทุกปี กลับกลายเป็นว่า บางปีขายได้มาก บางปีก็ขายได้น้อย เอาแน่นอนอะไรไม่ได้ พฤติการณ์ทำนองนี้การพยากรณ์ทางสถิติไม่สามารถทำได้
ตัวอย่างของการพยากรณ์จะดูได้จากรูปที่ ๑๑ โดยต่อเส้นแนวโน้มออกไปค่าที่อ่านได้บนแกนตั้ง ณ ปีที่ต้องการ คือ รายได้จากการขายผลิตภัณฑ์เคมี ซึ่งคาดว่า บริษัทดวงดี จำกัด จะได้รับโดยประมาณ ณ ปีนั้น
การพยากรณ์ทางสถิติอาจทำได้โดยการคำนวณจากสมการของแนวโน้ม (หาได้โดยวิธีกำลังสองน้อยที่สุด) สมมุติว่า แนวโน้มที่แสดงในรูปที่ ๑๑ มีสมการเป็น

