สมการและอสมการ

บางทีเราพบโจทย์บางประเภท เช่น "ชาวนาคนหนึ่งเลี้ยงหมู และ ไก่ ถ้านับหัวของสัตว์เหล่านี้จะได้ 20 หัว ถ้านับขาจะได้ 50 ขา ถามว่า เขามีหมูและไก่อย่างละกี่ตัว "

ถ้าให้ x แทนจำนวนหมู และ y แทนจำนวนไก่ เราจะได้สมการ 2 สมการคือ

x + y = 20 (จำนวนหัว) 
4x + 2y = 50 (จำนวนขา) 

เราต้องการหาค่าของ x และ y ซึ่งเมื่อนำไปแทนในสมการทั้งสองแล้วจะได้ข้อความจริงทั้งคู่ ในกรณีนี้ ถ้าแทน x ด้วย 5 และแทน y ด้วย 15 ในสมการทั้งคู่ จะได้ข้อความจริง เราจึงพูดว่า (5, 15) เป็นคำตอบของ ระบบสมการ (system of equations) ข้างต้น สมการทั้งสองเป็นสมการเชิงเส้นทั้งคู่ เราจึงเรียก ระบบสมการนี้ว่า ระบบสมการเชิงเส้น (system of linear equations)

ระบบสมการเชิงเส้นมีวิธีแก้หลายวิธี แต่ในที่นี้จะกล่าวถึงการแก้ระบบสมการด้วยวิธีเขียนกราฟ 

คำตอบ (5, 15) สำหรับระบบสมการในโจทย์ปัญหาเรื่องชาวนากับสัตว์ เลี้ยง หาได้จากกราฟ ดังนี้

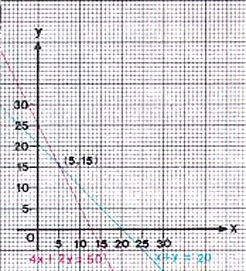
เขียนกราฟของสมการทั้งสองจะได้เส้นตรง 2 เส้น ทุกจุดบนเส้นตรงสีน้ำเงินเป็นคำตอบของสมการ x + y = 20 ทุกจุดบนเส้นตรงสีแดง เป็นคำตอบของ สมการ 4x + 2y = 50 จุดตัดคือ (5, 15) จึงเป็นคำตอบของสมการทั้งคู่พร้อมๆ กัน และ เป็นคำตอบของระบบสมการนี้

เราจึงสรุปได้ว่า ระบบสมการที่ประกอบด้วยสมการเชิงเส้น ที่มีตัวแปร 2 ตัว 2 สมการ อาจมีคำตอบเพียงคำตอบเดียว ในกรณีที่เส้นตรงทั้งสองตัดกัน  หรือไม่มีคำตอบเลยในกรณีที่เส้นตรงทั้งสองขนานกัน หรือมีคำตอบมากมายแจกแจงไม่หมดในกรณีที่เส้นตรงทั้งสองทับกัน

แม้ว่าระบบสมการที่มีตัวแปรไม่เกิน 2 ตัว จะไม่ใช่ระบบสมการเชิงเส้น เราก็อาจแก้ไขได้โดยวิธีเขียนกราฟ เช่น  

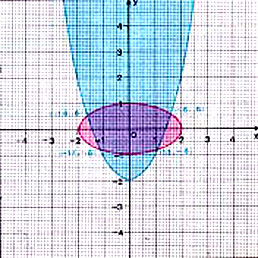
ระบบสมการเชิงเส้น
x^2  + 4y^2 = 4
y = x^2 - 2
มีคำตอบ 4 คำตอบ ค่าโดยประมาณคือ
(-1.1,-.8), (1.1,-8), (-1.6,.6), (1.6,.6)

สมการที่น่าสนใจประเภทหนึ่ง คือ สมการที่ต้องการคำตอบเฉพาะที่เป็นจำนวนเต็ม หรือจำนวนตักยะ สมการประเภทนี้เรียกว่า สมการไดโอแฟนทีน (Diophantine equations) ซึ่งเป็นชื่อที่ตั้งขึ้นเพื่อเป็นเกียรติแก่นักคณิตศาสตร์ชาวกรีกชื่อ ไดโอแฟนทัส *(Diophantus)

* ไดโอแฟนทัสมีชีวิตอยู่ในสมัยประมาณ 250 ปี ก่อนคริสต์ศักราช เป็นชาวเมืองอเล็กซานเดรีย เราไม่ค่อยทราบรายละเอียดเกี่ยวกับชีวิตของเขามากนัก แต่อาจจะคำนวณอายุของเขาได้จากคำซึ่งเล่ากันต่อๆ มาดังนี้ 
เขาเป็นเด็กอยู่ของอายุของเขาเป็นวัยรุ่นอยู่ 1/12 ของอายุ เป็นชายโสดอยู่ 1/7 ของอายุ ลูกชายของเขาเกิดเมื่อเขาแต่งงานแล้ว 5 ปี ลูกชายตายก่อนเขา 4 ปี เขามีอายุยืนเป็น 2 เท่าของลูกชาย (คำตอบคือ 84 ปี)

ตัวอย่างของโจทย์ปัญหาประเภทนี้คือ "มีส้มอยู่จำนวนหนึ่ง ถ้าจะแบ่งให้คน 5 คนๆละ เท่าๆกัน จะขาดส้ม 1 ผล ถ้าจะแบ่งให้คน 7 คนๆ ละเท่าๆกันก็จะขาด 1 ผล ถามว่ามีส้มอยู่เท่าไร"

ถ้าสมมุติว่า มีส้มอยู่ n ผล เราจะได้ว่า n+1 หารด้วย 5 ลงตัว และ หารด้วย 7 ก็ลงตัว นั่นคือ n+1 = 5x และ n+1 = 7y เมื่อ x และ y แทนจำนวนเต็มบวก 

เราจึงต้องแก้สมการ 5x = 7y เมื่อ x และ y แทนจำนวนเต็มบวก 

จะเห็นว่า สมการนี้มีคำตอบมากมายได้แก่ (7,5), (14,10), (21,15), (28,20), (35,25), (42,30),... คำตอบเหล่านี้ให้ค่า 5x (หรือ 7y) เป็น 35, 70, 105, 140, 175, 210,... ตามลำดับ ดังนั้นค่าของ n ที่ต้องการคือ 34, 69, 104, 139, 174, 209,... 

ถ้าโจทย์ถามเพิ่มเติมว่า จำนวนส้มน้อยที่สุดเป็นเท่าไร จึงจะมีลักษณะตามที่ต้องการก็จะได้คำตอบ 34 

สมการไดโอแฟนทีนมีอยู่มากมายหลายประเภท สมการไดโอแฟนทีน ที่มีชื่อเสียงมากสมการหนึ่งคือ สมการ x^2 + y^2= z^2 ซึ่งเราเรียกกันว่า สมการปีทาโกเรียน (Pythagorean equation) ชื่อนี้ตั้งขึ้นเพื่อเป็นเกียรติแก่ ปีทาโกรัส* (Pythagorus) การหาคำตอบที่เป็นจำนวนบวกของสมการนี้ก็คือ การหาความยาว ที่เป็นจำนวนเต็มของด้านทั้งสามของสามเหลี่ยมมุมฉากนั่นเอง คำตอบที่เราทราบ กันดีคือ x=3, y=4, z=5 ซึ่งเขียนได้อีกอย่างหนึ่งว่า (3,4,5) สมการปีทาโกเรียนนี้มีคำตอบมากมายนับได้ไม่หมด คำตอบทั้งหลายหาได้จากสูตร ต่อไปนี้คือ 

x = a^2 - b^2,y = 2ab และ z = a^2 + b^2 เมื่อ a และ b แทนจำนวน เต็ม เช่น ถ้าให้ a=2 และ b = 1 เราจะได้คำตอบ (3,4,5) ถ้าให้ a = 3 และ b = 2 เราจะได้คำตอบ (5,12,13) ถ้าให้ a = 3 และ b = 1 เราจะ ได้คำตอบ (8,6,10) เป็นต้น
 

* ปีทาโกรัส เป็นนักปรัชญา และ นักคณิตศาสตร์ชาวกรีกมีชีวิตอยู่ระหว่างปี 582 - 507 ปีก่อนคริสต์ศักราช ทฤษฎีบทของเขาซึ่งเรารู้จักกันดี คือทฤษฎีบทในเรขาคณิตที่กล่าวว่า กำลังสองของความยาวด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากใดๆ ย่อมเท่ากับผลบวกของกำลังสองของความยาวอีกสองด้าน

เรากล่าวได้ว่าสมการปีทาโกเรียนนั้น เราทราบคำตอบได้อย่างสมบูรณ์ เพราะเรามีวิธีหาคำตอบทั้งหมดได้

สมการไดโอแฟนทีนที่มีตัวแปร 2 ตัว และ เป็นการเชิงเส้น เช่น 5x = 7y, 6x + 15y = 12 ฯลฯ เราทราบคำตอบได้อย่างสมบูรณ์ แต่สมการไดโอแฟนทีนส่วนใหญ่ยังไม่ทราบคำตอบอย่างสมบูรณ์บางสมการยังไม่ทราบเลยด้วยซ้ำไปว่ามีคำตอบหรือไม่ เช่น สมการ x^n + y^n = z^n เมื่อ n เป็นจำนวนเต็ม ซึ่งมากกว่า 2 สมการนี้ไม่มีใครทราบเลยว่ามีคำตอบเป็นจำนวนเต็มบวกหรือไม่ 

แฟร์มาต์* ทำนายไว้ว่า "สมการ x^n + y^n = z^n ไม่มีคำตอบเป็นจำนวนเต็มบวก เมื่อ n เป็นจำนวนเต็มที่มากกว่า 2" ข้อความนี้เขียนได้อีกอย่างหนึ่ง ว่า "ไม่ว่า x, y, z, n จะเป็นจำนวนเต็มบวกใดๆ ก็ตาม ถ้า n มากกว่า 2 แล้ว จะได้ว่า x^n + y^n = z^n ข้อความนี้เรียกกันว่า ทฤษฏีบทสุดท้ายของแฟร์มาต์ (Fermat's Last Theorem) ในระยะเวลา 300 กว่าปีที่ผ่านมานี้ นักคณิตศาสตร์หลายคนพยายามพิสูจน์ข้อความนี้ และ มีผู้ค้นพบข้อความนี้เป็นข้อความจริง สำหรับหลายค่าของ n เช่น มีผู้พิสูจน์ได้ว่า "ไม่ว่า x,y,z,n จะเป็นจำนวนเต็มบวกใดๆ ก็ตาม ถ้า n มากกว่า 2 และ น้อยกว่า 100 แล้ว จะได้ว่า x^n + y^n = z^n แต่จนบัดนี้ก็ยังไม่มีใครสามารถพิสูจน์ได้ว่า ทฤษฎีบทสุดท้ายของแฟร์มาต์ เป็น ข้อความจริงหรือเท็จ

* แฟร์มาต์ (ค.ศ. 1601 - 1665) เป็นชาวฝรั่งเศส อาชีพรับราชการ งานอดิเรกคือ คณิตศาสตร์ ถือได้ว่าเป็นคนหนึ่งที่ริเริ่มเรขาคณิตวิเคราะห์ และ แคลคูลัส แต่ปัจจุบันคนรู้จัก เขามากจากผลงานของเขาเรื่องทฤษฎีของจำนวน (Theory of Numbers)

(1) ถ้านำจำนวนๆ หนึ่งมาบวก หรือ ลบทั้งสองข้างของเครื่องหมาย ซึ่ง แสดงความไม่เท่ากัน อสมการใหม่จะมีคำตอบเหมือนอสมการเดิม 
(2) ถ้านำจำนวนบวกมาคูณหรือหารทั้งสองข้างของเครื่องหมายซึ่งแสดง ความไม่เท่ากัน อสมการใหม่จะมีคำตอบเหมือนอสมการเดิม 
(3) ถ้านำจำนวนลบมาคูณทั้งสองข้างของเครื่องหมายซึ่งแสดงความมากกว่า อสมการใหม่ซึ่งมีคำตอบเหมือนอสมการเดิม จะต้องเชื่อมด้วยเครื่องหมาย ที่แสดงความน้อยกว่า 
(4) ถ้านำจำนวนลบ มาคูณหรือหารทั้งสองข้างของเครื่องหมายซึ่งแสดง ความน้อยกว่า อสมการใหม่ซึ่งมีคำตอบเหมือนอสมการเดิม จะต้องเชื่อมด้วย เครื่องหมายที่แสดงความมากกว่า

อสมการอาจมีตัวแปรมากกว่า 1 ตัวแปรก็ได้ และ วิธีแก้อสมการที่มี ตัวแปรไม่เกิน 2 ตัวแปรเราสามารถใช้วิธีกราฟได้ ดังตัวอย่างต่อไปนี้ 

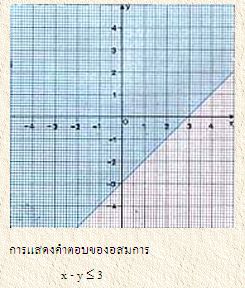
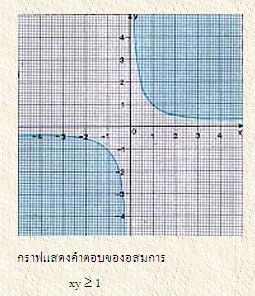
เราอาจจะใช้วิธีกราฟ แก้ระบบอสมการได้ ดังต่อไปนี้

ต่อไปนี้เป็นตัวอย่างของการแก้ปัญหาระบบอสมการเชิงเส้นที่มีเงื่อนไข เพิ่มเติมบางอย่าง

สวนขนัดหนึ่งมีพื้นที่สำหรับปลูกทุเรียนได้ 30 ต้น เจ้าของสวนต้องการปลูกทุเรียน 2 พันธุ์คือ ชะนี และ รวง การปลูกใช้กิ่งทาบ ชะนีราคากิ่งละ 25 บาท รวงราคากิ่งละ 10 บาท ชะนีจะให้ผลในเวลา 7 ปี รวงให้ผลในเวลา 5 ปี ชะนี ให้ผลประมาณ 25 ผลต่อต้น ส่วนรวงให้ผลประมาณ 50 ผลต่อต้นชะนีขายได้ โดยเฉลี่ยผลละ 45 บาท รวงขายได้โดยเฉลี่ยผลละ 20 บาท หลังจากทุเรียนให้ ผลเต็มที่แล้ว ชาวสวนต้องการมีรายได้ประจำปีจากการขายทุเรียนมากที่สุด เขาควรปลูกทุเรียนอย่างละกี่ต้น ถ้าเขามีงบประมาณค่าซื้อกิ่งเพียง 500 บาท  

ภายใต้เงื่อนไขสองข้อนี้ เขาต้องการให้รายได้ประจำปีสูงสุด ชะนีจะให้ รายได้ต้นละ 1,125 บาทต่อปี รวงจะให้รายได้ต้นละ 1,000 บาทต่อปี ดังนั้นหลังจากที่ทุเรียนทุกต้นให้ผลเต็มที่แล้ว เขาจะมีรายได้ 1125x + 1000y บาท ต่อปี

ฉะนั้น เราต้องการหาค่า x และ y ที่เป็นไปตามเงื่อนไขข้อ (1) และข้อ (2) และทำให้ 1125x + 1000y มีค่าสูงสุดด้วย นอกจากนี้ยังมีเงื่อนไขที่ละไว้ในฐานที่เข้าใจอีกด้วยว่า x และ y ต้องแทนจำนวนเต็มซึ่งไม่น้อยกว่า 0 เนื่องจาก x และ y แทนจำนวนต้นไม้

ถ้าปริมาณๆ หนึ่ง ตัวแปรที่ปรากฏในปริมาณนั้นมีเลขชี้กำลังเป็น 1 และ ตัวแปรไม่คูณกันเลย การหาคำตอบซึ่งทำให้ปริมาณนั้นมีค่าสูงสุดหรือต่ำสุด ภาย ใต้เงื่อนไขที่เขียนได้ในรูปอสมการเชิงเส้น เราเรียกว่า กำหนดการเชิงเส้น

ปัจจุบันมีตำรามากมายเกี่ยวกับกำหนดการเชิงเส้น และ ในตำราเหล่านั้น ได้บอกวิธีแก้ปัญหาหลายวิธี ในที่นี้เราจะใช้วิธีเขียนกราฟ ดังต่อไปนี้

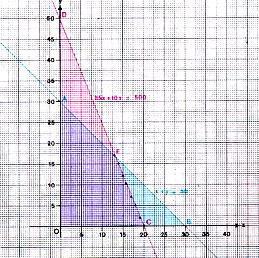
ฉะนั้น คำตอบของระบบอสมการ (1) และ (2) จะอยู่ในบริเวณ รูปสี่เหลี่ยม OAEC ในบรรดาคำตอบเหล่านี้ เราจะต้องหาคำตอบที่ทำให้ 1125x +1000y มีค่าสูงสุด คำตอบเหล่านี้จะต้องให้ค่า x และ y เป็นจำนวนเต็ม ทั้งคู่ด้วย 

ถ้าไม่คิดอะไรเลย เราก็อาจจะหาคำตอบนั้นได้ดังนี้ หาจุดทั้งหมดในบริเวณสี่เหลี่ยม OAEC ซึ่งมีทั้ง x และ y เป็นจำนวนเต็ม (มีอยู่ไม่เกิน 600 จุด) หาค่า 1125x + 1000y ของแต่ละจุด จุดที่ให้ค่ามากสุดคือ คำตอบที่ต้องการ 

แต่ถ้าเราใช้ความคิดเพียงเล็กน้อย เราก็จะไม่ต้องพิจารณาจุดทั้งหมดใน บริเวณดังกล่าว เพราะจุดสองจุดใดๆ ซึ่งอยู่ในแนวนอนแนวเดียวกัน (ค่า y เท่า กัน) จุดทางขวา (ค่า x มากกว่า) จะให้ค่า 1125x + 1000y มากกว่าจุดทางซ้าย ในทำนองเดียวกันจุดสองจุดใดๆ ซึ่งอยู่ในแนวตั้งแนวเดียวกัน (ค่า x เท่ากัน) จุดที่อยู่เหนือ (ค่า y มากกว่า) จะให้ค่า 1125x + 1000y มากกว่า ดังนั้นจุดที่จะ ให้ค่า 1125x + 1000y มากๆ ควรจะเป็นจุดที่อยู่บนขอบ AE และ EC หรือจุดที่อยู่ ใกล้ๆขอบทั้งสองนี้เท่านั้น จุดเหล่านี้แสดงไว้ในกราฟ 

นอกจากนี้ เรายังสังเกตได้อีกว่า ถ้าพิจารณาจุด (x,y) จุดหนึ่งในบรรดา จุดเหล่านี้บนเส้น AE เช่น (5,25) จุดที่อยู่ถัดไปทางขวาคือจุด (x + 1, y - 1) จะให้ค่า 1125x + 1000y มากกว่า ดังนั้น ในบรรดาจุดเหล่านี้ที่อยู่บน AE จุด (13,17) ซึ่งอยู่ขวาสุด จะให้ค่า 1125x + 1000y มากที่สุด 

ดังนั้นเราคำนวณค่า 1125x + 1000y ของจุดต่างๆ ที่เหลือ แล้วนำมาเทียบ กับค่าที่ได้จากจุด (13,17) ดังนี้ 

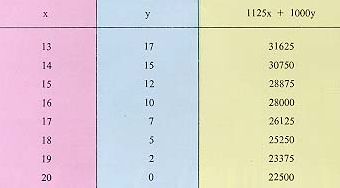
เราสรุปได้ว่า จุด (13,17) ให้ค่า 1125x + 1000y สูงสุด นั่นคือ ชาวสวนควรจะปลูกชะนี 13 ต้น และปลูกรวง 17 ต้น จึงจะได้รายได้ประจำปีสูงสุด 

ถ้าชาวสวนต้องการรายได้ภายใน 10 ปีสูงสุด เขาจะต้องหาค่า x และ y ซึ่งทำให้ (3 x 45 x 25X) + (5 x 20 x 50y) หรือ 3375X + 5000y สูงสุด คำตอบจะเป็น (0,30) นั่นคือ เขาต้องปลูกรวงหมดทั้งหมดทั้งสวนในกรณีนี้   

กำหนดการเชิงเส้นนี้เป็นส่วนหนึ่งของวิชาวิจัยปฏิบัติการ (Operations Research) ซึ่งมีประโยชน์มากสำหรับการวางแผนในวงการต่างๆ เช่น เกษตรกรรม อุตสาหกรรม การขนส่ง ปัจจุบันวิชานี้มีสอนในระดับอุดมศึกษาของสถาบันหลายแห่งในประเทศไทย