ฟังก์ชัน

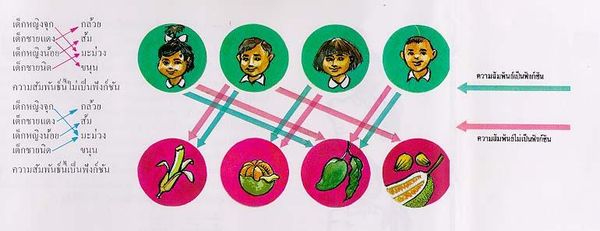
ในชีวิตประจำวัน แต่ละคนจะต้องเกี่ยวข้องกับบุคคล และ สิ่งต่างๆ อยู่ตลอดเวลา เริ่มตั้งแต่ตื่นนอนในตอนเช้า กิจวัตรที่จะต้องทำ ก็คือ แปรงฟัน ล้างหน้า อาบน้ำ แต่งตัว รับประทานอาหาร ไปโรงเรียน หรือ ไปทำงาน สิ่งของที่เราจะต้องเกี่ยวข้องด้วยก็คือ แปรงสีฟัน ยาสีฟัน สบู่ น้ำ เสื้อผ้า อาหาร ฯลฯ บุคคลที่จะต้องเกี่ยวข้องด้วยก็มี บิดา มารดา พี่ น้อง ครู เพื่อนนักเรียน หรือ เพื่อนร่วมงาน ฯลฯ แต่ถ้าใครถามเราว่า "ความเกี่ยวข้อง" คืออะไร เราคงไม่ทราบว่าจะตอบอย่างไร เมื่อพิจารณาดูความเกี่ยวข้องใดความเกี่ยวข้องหนึ่ง สิ่งที่เราอาจเห็นได้ หรือ ทราบได้ก็คือ สิ่งที่มีความเกี่ยวข้องนั้นๆ ต่อกัน เช่น "การชอบรับประทาน" เป็นความเกี่ยวข้องอย่างหนึ่ง เรามองไม่เห็นการชอบรับประทาน แต่เราทราบว่า เด็กหญิงจุกชอบรับประทานมะม่วง เด็กชายแดงชอบรับประทานกล้วย และ ขนุน เด็กหญิงน้อยชอบรับประทานส้ม และ เด็กชายนิดชอบรับประทานมะม่วง เป็นต้น เราทราบแต่เพียงว่า เด็กคนไหนเกี่ยวข้องกับผลไม้ชนิดใดด้วย "การชอบรับประทาน" ในที่นี้ก็คือ
 

เด็กหญิงจุก, มะม่วง

เด็กชายแดง, กล้วย

เด็กชายแดง, ขนุน

เด็กหญิงน้อย, ส้ม

เด็กชายนิด, มะม่วง

 

จะเห็นว่าความเกี่ยวข้องหนึ่งๆ ทำให้เกิดการจับคู่ของสิ่งต่างๆ สองพวกที่มีความเกี่ยวข้องนั้นๆ ต่อกัน

 

 

 

 

เรื่อง "ความเกี่ยวข้อง" นี้ เป็นเรื่องสำคัญที่เป็นประโยชน์ ในการศึกษาวิชาการหลายสาขาวิชา เพื่อให้วิชาคณิตศาสตร์เป็นประโยชน์ ต่อวิชาการต่างๆ อย่างกว้างขวาง นักคณิตศาสตร์จึงนำเรื่อง "ความเกี่ยวข้อง" มาศึกษาเป็นพิเศษ ในวิชาคณิตศาสตร์เราเรียก "ความเกี่ยวข้อง" ว่า "ความสัมพันธ์" ดังนั้น ความสัมพันธ์ก็คือ ความเกี่ยวข้อง ซึ่งบอกให้เราทราบว่า แต่ละสมาชิกในเซตแรก เกี่ยวข้องกับสมาชิกใดบ้างในเซตที่สอง ดังตัวอย่างที่กล่าวข้างต้น เซตแรกก็คือ เซตของเด็ก และ เซตที่สองคือเซตของผลไม้

 

ในบางกรณีเซตสองเซตที่มีความสัมพันธ์กันนั้น สมาชิกแต่ละสมาชิกในเซตแรกมีความสัมพันธ์กับสมาชิก ในเซตที่สองเพียงสมาชิกเดียวเป็นอย่างมาก ในกรณีเช่นนี้เรากล่าวว่า ความสัมพันธ์นั้นเป็น ฟังก์ชัน จากเซตที่หนึ่ง ไปยังเซตที่สอง จากตัวอย่างความสัมพันธ์ของเซตของเด็ก กับเซตของผลไม้นั้น จะเห็นว่า เด็กหญิงจุกมีความสัมพันธ์กับมะม่วงอย่างเดียว เด็กหญิงน้อยมีความสัมพันธ์กับส้มอย่างเดียว เด็กชายนิดมีความสัมพันธ์กับมะม่วงอย่างเดียว แต่เด็กชายแดงมีความสัมพันธ์กับกล้วย และ ขนุน ซึ่งเกิดหนึ่งสิ่ง ดังนั้น ความสัมพันธ์จากเซตของเด็กไปยังเซตของผลไม้จึงไม่เป็นฟังก์ชัน แต่ถ้าเด็กชายแดงชอบรับ ประทานกล้วยเพียงอย่างเดียว ความสัมพันธ์ระหว่างสองเซตนี้ ก็จะเป็นฟังก์ชัน แสดงได้โดยแผนผังดังนี้

 

 

 

 

การกำหนดความสัมพันธ์ระหว่างสิ่งต่างๆ นั้น อาจทำได้หลายวิธีด้วยกัน วิธีกำหนดความสัมพันธ์ซึ่งเข้าใจกันโดยง่ายวิธีหนึ่งก็คือ การกำหนดความสัมพันธ์โดยการแสดงด้วยตาราง หรือบัญชีรายการ เช่น การทำรายการราคาอาหาร ก็เป็นการกำหนดความสัมพันธ์ระหว่างชนิดของอาหารกับราคาอาหาร เช่น 

 

 

 

นักคณิตศาสตร์นิยมเขียนแสดงการจับคู่ของสิ่งที่มีความสัมพันธ์กัน โดยเขียนชื่อของสิ่งคู่ที่มีความสัมพันธ์กันนั้นไว้ในเครื่องหมาย ( ) โดยเขียนชื่อสมาชิกที่มาจากเซตที่หนึ่งไว้ข้างหน้า และ เขียนชื่อสมาชิกที่มาจากเซตที่สองไว้ข้างหลัง และ คั่นชื่อทั้งสองด้วยเครื่องหมาย , เช่น ในการแสดงความสัมพันธ์ระหว่างอาหารกับราคาอาหาร ถ้าข้าวราดแกง มีราคา 5 บาท เขียนแสดงด้วยสัญลักษณ์ได้ดังนี้

(ข้าวราดแกง, 5 บาท)

เรียกวงเล็บคู่ของสมาชิกที่นำมาจากเซตที่หนึ่ง และ เซตที่สองซึ่งเขียนเรียงไว้ตามลำดับเช่นนี้ว่า คู่ลำดับ ดังนั้น ความสัมพันธ์ระหว่างสองเซต จึงก่อให้เกิดเซตของคู่ลำดับของเซตที่มีความสัมพันธ์กัน จากตัวอย่างของความสัมพันธ์ ระหว่างเซตของอาหารกับเซตของราคาอาหาร เมื่อนำความสัมพันธ์มาเขียนเป็นคู่ลำดับแล้วจะได้เซตของคู่ลำดับดังนี้

{(ข้าวราดแกง, 5 บาท), (ข้าวราดแกง, 7 บาท) (ก๋วยเตี๋ยวผัด, 8 บาท) (ขนม, 2 บาท) (น้ำแข็งเปล่า, 0.50 บาท)}

ดังนั้น อาจกล่าวได้ว่า ความสัมพันธ์ระหว่างเซต ก กับเซต ข ใดๆ ก็คือ กฎเกณฑ์ที่ก่อให้เกิดการจับคู่ระหว่างสมาชิกของเซต ก กับสมาชิกของเซต ข และ กฎเกณฑ์นี้ทำให้เกิดเซตของคู่ลำดับขึ้นมาเซตหนึ่ง โดยที่ในแต่ละคู่อันดับเหล่านี้ ตัวหน้าเป็นสมาชิกในเซต ก ตัวหลังเป็นสมาชิกในเซต ข ด้วยเหตุนี้นักคณิตศาสตร์จึงถือเอาเซตของคู่ลำดับของสิ่งที่เกี่ยวข้องกันเป็นสิ่งสำคัญ และ ให้นิยามความสัมพันธ์ดังนี้

"ความสัมพันธ์ระหว่างเซต ก กับเซต ข ใดๆ คือ เซตของคู่ลำดับซึ่งมีสมาชิกจากเซต ก เป็นตัวหน้า และสมาชิก จากเซต ข เป็นตัวหลัง"

เนื่องจากฟังก์ชันเป็นความสัมพันธ์ ดังนั้นฟังก์ชันจึงเป็นเซตของคู่ลำดับด้วย เราให้นิยามของคำว่า ฟังก์ชัน จากเซต ก ไปยังเซต ข ได้ดังนี้

"ฟังก์ชันจากเซต ก ไปยังเซต ข ก็คือ เซตของคู่ลำดับที่สมาชิกจากเซต ก เป็นตัวหน้าในคู่ลำดับ และ สมาชิก จากเซต ข เป็นตัวหลังในคู่ลำดับ โดยที่แต่ละสมาชิกของเซต ก จะปรากฏอยู่ในคู่ลำดับกับสมาชิกจากเซต ข ได้เพียงสมาชิกเดียวเท่านั้น"
 

 

 

 

บางครั้งอาจกำหนดความสัมพันธ์โดยการพูดหรือเขียนเพียงข้อความสั้นๆ เช่น กำหนดราคาลูกกวาดไว้ว่า ราคา 3 ลูกต่อ 1 บาท (100 สตางค์) แต่ถ้าซื้อไม่ครบ 3 ลูก คิดลูกละ 40 สตางค์ ก็อาจจะทราบได้ว่า ราคาลูกกวาดสัมพันธ์กับจำนวนลูกกวาดอย่างไร ผู้ที่รู้เลขคณิตเบื้องต้นจะคิดได้ง่ายว่า ราคาลูกกวาดสัมพันธ์กับจำนวนลูกกวาด ตามตารางข้างล่างนี้
 

จำนวนลูกกวาด	1	2	3	4	5	6	7	8	9	10
ราคา (สตางค์)	40	80	100	140	180	200	240	280	300	340

นอกจากนี้ยังสามารถคิดต่อไปได้ว่า ถ้าลูกกวาดมีจำนวนเป็นอย่างอื่น ที่ไม่ได้บ่งไว้ในตารางนี้ จะมีราคาเป็นเท่าใด

 

จะเห็นได้ว่า วิธีกำหนดความสัมพันธ์วิธีนี้ ช่วยให้เราสามารถแสดงความสัมพันธ์จำนวนต่างๆ ได้มากมายด้วยข้อความสั้นๆ เพียงไม่กี่คำ เราเรียกวิธีการนี้ว่า วิธีกำหนดความสัมพันธ์ด้วยสูตร และ เรียกข้อความสั้นๆ ซึ่งเราใช้กำหนดความสัมพันธ์ว่า สูตร

จากตัวอย่างดังกล่าวข้างต้น ถ้าให้ ก แทนจำนวนลูกกวาด และ ค แทนราคาลูกกวาด จะเขียนเป็นสูตรได้ดังนี้ 

 

 

 

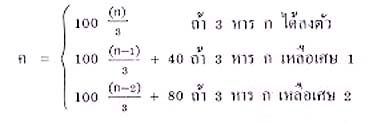
ในกรณีที่ฟังก์ชันเป็นความสัมพันธ์ระหว่างปริมาณต่างๆ การใช้สูตร กำหนหดฟังก์ชันจะทำให้ง่ายขึ้น เช่น ความยาวของด้าน ของรูปสี่เหลี่ยมจตุรัส กับพื้นที่ของรูปสี่เหลี่ยมจตุรัสมีความสัมพันธ์กันด้วยสูตร 

พ = ด x ด  
   = ด^2

โดยที่ พ แทนพื้นที่ และ ด แทนความยาวของด้าน

ในที่นี้จะเห็นว่าเมื่อกำหนดค่า ด เป็นจำนวนใดจำนวนหนึ่ง จะหาค่า พ ได้หนึ่งค่า และเมื่อค่า ด เปลี่ยนไปค่า พ ก็เปลี่ยนตามไปด้วย ดังแสดงได้ด้วย ตารางต่อไปนี้ 

 

 

ตัวอักษรที่ใช้แทนค่าที่เปลี่ยนได้ เช่น ตัว ด และ พ ในตัวอย่างนั้นเรียกว่า ตัวแปรค่า หรือ ตัวแปร

อาจนำฟังก์ชันหรือความสัมพันธ์ระหว่างปริมาณต่างๆ มาแสดงให้เข้าใจ ได้ง่ายๆ โดยการแสดงด้วยกราฟ การแสดงฟังก์ชัน หรือความสัมพันธ์ด้วยกราฟ นี้ ทำได้โดยเขียนแทนคู่ลำดับคู่หนึ่งด้วยจุดในระนาบ เช่น ในความสัมพันธ์ ระหว่างพื้นที่ กับความยาว ของด้านของรูปสี่เหลี่ยมจตุรัสนั้น ความยาวของด้าน ด กับพื้นที่ พ ประกอบกันเป็นคู่ลำดับ (พ, ด) ความสัมพันธ์นี้คือ 

{(1,1), (1.1,1.21), (1.5, 2.25), (2,4), (3,9),...} 

เมื่อนำคู่ลำดับเหล่านี้แทนด้วยจุดในระนาบจะได้กราฟ ดังรูปต่อไปนี้

 

 

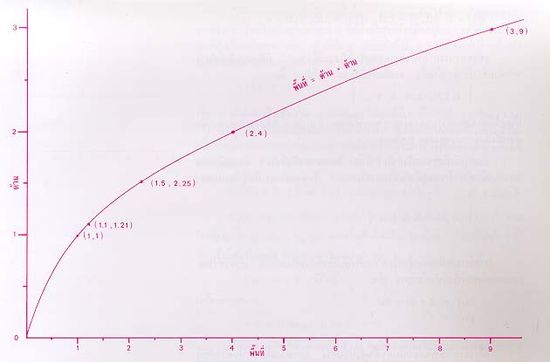
เนื่องจากฟังก์ชันเป็นเซตของคู่ลำดับ และนิยมใช้อักษรแทนเซต ดังนั้น จึงใช้อักษรแทนฟังก์ชันด้วย เช่น ความสัมพันธ์ ระหว่างพื้นที่สี่เหลี่ยมจตุรัสกับความยาวด้าน ที่กล่าวมาข้างต้น เป็นความสัมพันธ์ที่เป็นฟังก์ชัน ถ้าแทนฟังก์ชันนี้ ด้วยอักษร f ดังนั้น 

f = {(1,1), (1.1,1.21), (1.5,2.25), (2,4), (3,9),...} 

สมาชิกตัวหลังในคู่ลำดับต่างๆ ของเซต f คือ ค่า ของฟังก์ชัน f ดังในตัวอย่าง จะเห็นว่า 1 เป็นค่าของฟังก์ชัน f ที่ 1,1.21 เป็นค่าของฟังก์ชัน f ที่ 1.1, 4 เป็นค่าของฟังก์ชัน f ที่ 2 ฯลฯ โดยทั่วๆ ไป ถ้า (x,y) เป็นคู่ลำดับในเซต f แล้ว y เป็นค่าของฟังก์ชัน f ที่ x และ เขียนแทน y ด้วย f (x) หรือ y = f (x) สำหรับฟังก์ชัน f ในตัวอย่างเขียนได้ดังนี้ 

f (1) = 1, f(1.1) = 1.21, f(1.5) = 2.25 f(2) = 4...ฯลฯ

เซตของบรรดาค่าทั้งหลายของฟังก์ชัน f มีชื่อว่า พิสัยของฟังก์ชัน f จากตัวอย่างที่กล่าวข้างต้น จะเห็นว่าพิสัยของฟังก์ชัน f คือ 

{ 1, 1.21, 2.25, 4, 9,... } 

ถ้าจะให้คำจำกัดความอย่างง่ายๆ ของพิสัยของฟังก์ชัน f ก็คือเซตของสมาชิก ตัวหลังในคู่ลำดับของเซต f นั่นเอง 

สิ่งที่คู่กับพิสัยของฟังก์ชัน f ก็คือ โดเมนของฟังก์ชัน f ซึ่งจะเป็นเซต ของสมาชิกตัวหน้าของคู่ลำดับทั้งหลายในเซต f ในตัวอย่างจะเห็นว่า โดเมนของ ฟังก์ชัน f คือ 

{ 1, 1.1, 1.5, 2, 3,...} 

การกำหนดฟังก์ชันซึ่งเป็นความสัมพันธ์ระหว่างจำนวนนั้น มักจะทำโดย การแทนค่าของฟังก์ชันด้วยสูตร เช่น 

f (x) = 2 + 3x + 5x^2
g (x) = 2x^x 

เนื่องจากฟังก์ชันเช่นนี้มีค่าเป็นจำนวนจริง และ ตัวแปร x เป็นตัวแปรที่ ใช้แทนจำนวนจริง ฟังก์ชันเช่นนี้เรียกว่า ฟังก์ชันค่าจริงของตัวแปรจริง (real valued function of real variable) ซึ่งอาจจำแนกฟังก์ชันประเภทนี้ ตามคุณสมบัติของสูตร ที่กำหนดค่าของฟังก์ชัน

 

 

ฟังก์ชัน f ใดๆ ถ้าสามารถบอกค่าของฟังก์ชันนั้นได้ด้วยสูตรต่อไปนี้เรียก ว่าเป็นฟังก์ชันโพลิโนเมียล (polynomial function) 

f (x) = ao + a1x + a2x^2 + ... + anxn โดยที่ ao, a1, ...,an เป็นค่าคงที่ 

ตัวอย่างของฟังก์ชันโพลิโนเมียล ได้แก่ 

f (x) = 2 - 7x + 5x^2 
g (x) = 2 + 8x 
h (x) = 7 

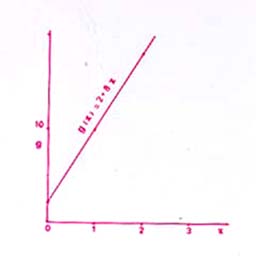
ถ้าเขียนกราฟของฟังก์ชันเหล่านี้ดู จะสังเกตเห็นได้ว่า ถ้าสูตรของค่าของฟังก์ชันโพลิโนเมียลไม่มีพจน์ x ที่มีกำลังสูงกว่าหนึ่งอยู่เลย จะได้กราฟของฟังก์ชันเป็นเส้นตรง เช่น ฟังก์ชัน g และฟังก์ชัน h จะมีกราฟเป็นเส้นตรง ฟังก์ชันโพลิโนเมียลที่ค่าของฟังก์ชันเขียนได้ในรูป 

f (x) = a + bx 

เรียกว่า ฟังก์ชันเชิงเส้น (linear function) ในกรณีที่ b เป็นศูนย์ กราฟของ f (x) = a จะเป็นเส้นตรงขนานกับแกนในแนวนอน ซึ่งแสดงว่าค่าของฟังก์ชัน f ไม่ เพิ่มขึ้นหรือลดลงตามค่าของ x เลย ฟังก์ชันเช่นนี้เรียกว่า ฟังก์ชันคงที่ (constant function)

 

ฟังก์ชัน f ใดๆ ที่มีค่า f(x) คล้องตามสมการในรูป 

P0(x) + P1(x) f(x) + P2(x) ( f(x) )^2 +... + Pn(x) ( f(x) )^n = 0 
โดยที่ P0(x), P1(x), ..., Pn (x) ต่างเป็นฟังก์ชันโพลิโนเมียล เรียกฟังก์ชัน f นี้ ว่า ฟังก์ชันพีชคณิต (algebraic function) เช่น 

 

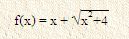
คล้องตามสมการ 

4 + 2x (f(x)) - (f(x))^2 = 0 

ถ้าสมการที่ฟังก์ชันพีชคณิต f(x) คล้องตามนั้นไม่ยุ่งยากนักจะแก้สมการ หาสูตรของ f(x) ได้ในรูปของรากกำลังต่างๆ ของ P0(x), P1(x),... Pn(x) แต่ โดยทั่วๆ ไปแล้ว จะแก้สมการหาสูตรของ f(x) ในพจน์ของ P0(x),...,Pn(x) ไม่ได้ ในกรณีพิเศษที่สมการดังกล่าวเป็นสมการในรูป 

 

 

 

ฟังก์ชันพีชคณิตประเภทนี้เรียกว่า ฟังก์ชันตรรกยะ (rational function)   

จะเห็นได้ว่าฟังก์ชันตรรกยะก็คือฟังก์ชันที่สามารถเขียนในรูปของเศษส่วน ของค่าของฟังก์ชันโพลิโนเมียลสองฟังก์ชันได้นั่นเอง ในเศษส่วนดังกล่าวนี้ฟังก์- ชันที่เป็นส่วนอาจเป็นฟังก์ชันที่มีค่าคงที่ ในกรณีเช่นนี้ฟังก์ชันตรรกยะก็เป็นฟังก์ชันโพลิโนเมียลนั่นเอง ดังนั้นบรรดาฟังก์ชันโพลิโนเมียลทั้งหลายต่างก็เป็นพังก์ชัน พีชคณิตด้วย ด้วยเหตุนี้คำว่าฟังก์ชันพีชคณิต จึงมีความหมายครอบคลุมไปถึงฟังก์ชันต่างๆ อีกมากมาย แต่อย่างไรก็ตามก็ยังมีฟังก์ชันที่ไม่ใช่ฟังก์ชันพีชคณิต อีกมาก เช่น ฟังก์ชัน f(x) = 2^x, g(x) = log x, h(x) = sin x ฯลฯ ฟังก์ชันที่ ไม่ใช่ฟังก์ชันพีชคณิตเหล่านี้ เรียกว่า ฟังก์ชันอดิศัย (transcendental function)