เซต

ในชีวิตประจำวันของเรา ใช้คำต่างๆ กัน เมื่อกล่าวถึงกลุ่มของสิ่งต่างๆ เช่น ฝูงนก โขลงช้าง คณะรัฐมนตรี สำรับกับข้าว เป็นต้น ในวิชาคณิตศาสตร์ เราใช้เซตเพียงคำเดียวเท่านั้น เมื่อบ่งถึงกลุ่มของสิ่งต่างๆ

นี่คือฝูงนก ซึ่งจะเรียกว่า เซตของนก

นี่คือช้างโขลงหนึ่ง ซึ่งจะเรียกว่า เซตของช้าง

เซตหนึ่งๆ ไม่จำเป็นจะต้องประกอบด้วยของชนิดเดียวกัน ดังตัวอย่างต่อไปนี้ 

นี่คือเซตที่ประกอบด้วยหนูหน่อยกับของเล่นของเขา

เซตอาจประกอบด้วยเซตต่างๆ ก็ได้ เช่น เซตของทีมฟุตบอลที่เข้าร่วมการแข่งขันเอเชียนเกมในปีพ.ศ. 2521 (ทีมฟุตบอลเป็นเซตของนักฟุตบอล)

อ่านว่า หนูหน่อย เป็นสมาชิกของเซต ที่ประกอบด้วย หนูหน่อย คุณพ่อ คุณแม่ และ น้องชาย

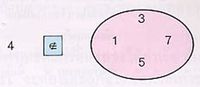
อ่านว่า 4 ไม่เป็นสมาชิกของเซต ที่ประกอบด้วย 1, 3, 5, 7

การเขียนเซต

ในการเขียนเซต นอกจากจะเขียนวงกลมหรือวงรีล้อมรอบสมาชิกทั้งหมด ของเซตไว้ดังที่แสดงมาแล้ว เรายังมีวิธีเขียนเซตแบบอื่นอีก คือ 

1. วิธีแจกแจงสมาชิก 

วิธีนี้ เราเขียนสมาชิกทั้งหมดลงในเครื่องหมายวงเล็บปีกกา และคั่นระหว่างสมาชิกด้วยเครื่องหมายจุลภาค เช่น

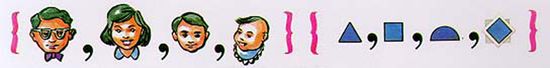
ถ้าเซตมีสมาชิกมากมายไม่สิ้นสุดเราใช้ "..." เพื่อบอกว่ายังมีสมาชิกตัวอื่นๆ อยู่ในเซตนี้ด้วย เช่น เซตของจำนวนนับ เขียนแทนด้วย {1, 2, 3,...} แต่ถ้าเซตมีสมาชิกมาก และ มีสมาชิกสุดท้าย เราใช้ "...," แล้วตามด้วยสมาชิกสุดท้าย เช่น เซตของจำนวนเต็มบวกที่น้อยกว่า 100 เขียนแทนด้วย {1, 2, 3,..., 99}

2. วิธีบ่งลักษณะของสมาชิก 

วิธีนี้ เราเขียนตัวแปรตัวหนึ่งแทนสมาชิกของเซตไว้ในวงเล็บปีกกา พร้อมทั้งมีคำอธิบายคุณสมบัติของสมาชิกที่อยู่ในเซตนั้น เช่น

เซตของวันในหนึ่งสัปดาห์ เขียนแทนด้วย { x | x เป็นวันในหนึ่งสัปดาห์ } 
อ่านว่า เซตของ X ซึ่งมีคุณสมบัติว่า X เป็นวันใดๆ ในหนึ่งสัปดาห์

{1, 2, 3} เขียนแทนด้วย { x | x เป็นจำนวนเต็มบวก และ x<4 }
อ่านว่า เซตของ x ซึ่งมีคุณสมบัติว่า x เป็นจำนวนเต็มบวกใดๆ ที่มีค่าน้อยกว่า 4

เซตของจำนวนจริงที่อยู่ระหว่าง 0 และ 1 เขียนแทนด้วย { x | x เป็นจำนวนจริง และ 0 < x < 1 } 
อ่านว่า เซตของ x ซึ่งมีคุณสมบัติว่า x เป็นจำนวนจริงที่มีค่ามากกว่า 0 และ น้อยกว่า 1

 

เพื่อความสะดวกในการอ้างถึงเซตต่างๆ อาจกำหนดชื่อเซตนั้นด้วยตัวอักษร เช่น 

A = { 1, 2, 3,..., 99 } 
B = { x | x เป็นจำนวนเต็มบวก และ x < 4 }

Content